网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
已知平面直角坐标系内一个圆,其方程为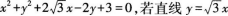 沿x轴平移后与圆相切,则移动后的直线在Y轴上最小的截距是( )
沿x轴平移后与圆相切,则移动后的直线在Y轴上最小的截距是( )
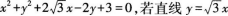 沿x轴平移后与圆相切,则移动后的直线在Y轴上最小的截距是( )
沿x轴平移后与圆相切,则移动后的直线在Y轴上最小的截距是( )
A.-2
B.-6
C.2
D.6
B.-6
C.2
D.6
参考答案
参考解析
解析:

更多 “已知平面直角坐标系内一个圆,其方程为沿x轴平移后与圆相切,则移动后的直线在Y轴上最小的截距是( ) A.-2 B.-6 C.2 D.6” 相关考题
考题
若方程Y=a+bX中的截距a
若方程Y=a+bX中的截距aA、随着X的增大,Y增大B、随着X的增大,Y减少C、随着X的减少,Y减少D、回归直线与Y轴的交点在原点下方E、回归直线与Y轴的交点在原点上方
考题
在平面直角坐标系中,以坐标原点0为极点,x轴的正半轴为极轴建立极坐标系。已知 点A的极坐标为.直线Z的极坐标方程为且点A在直线Z上。
(1)求。的值及直线Z的直角坐标方程;
(2)圆C的参数方程为试判断直线Z与圆C的位置关系。
考题
填空题高斯平面直角坐标系是以每一带的轴子午线的投影为x轴,赤道的投影为y轴,各个投影带自成一个平面直角坐标系统,其中x轴向()为负。
热门标签
最新试卷