网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设二叉排序树上有n个结点,则在二叉排序树上查找结点的平均时间复杂度为()。


参考答案
参考解析
解析: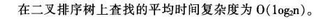
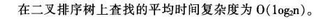
更多 “设二叉排序树上有n个结点,则在二叉排序树上查找结点的平均时间复杂度为()。 ” 相关考题
考题
在具有n个结点的二叉排序树上插入一个新结点时,根据n个数据元素生成一棵二叉排序树时,其时间复杂性大致为______。A.O(n)B.O(n2)C.O(log2n)D.O(nlog2n)
考题
结点数目为n的二叉查找树(二叉排序树)的最小高度为(56)、最大高度为(57)。A.AB.B
结点数目为n的二叉查找树(二叉排序树)的最小高度为(56)、最大高度为(57)。A.AB.BC.CD.D
考题
以下关于二叉排序树(或二叉查找树、二叉搜索树)的叙述中,正确的是( )A.对二叉排序树进行先序、中序和后序遍历,都得到结点关键字的有序序列B.含有N个结点的二叉排序树高度为【log2n】+1C.从根到任意二个叶子结点的路径上,结点的关键字呈现有序排列的特点D.从左到右排列同层次的结点,’其关键字呈现有序排列的特点
考题
关于二叉排序树描述有误的是()。A、二叉排序的右子树上结点的关键字小于左子树上的结点的关键字B、二叉排序的左子树上结点的关键字小于右子树上的结点的关键字C、二叉排序的根节点的关键大于右子树上结点的关键字D、二叉排序的根节点的关键大于左子树上结点的关键字
考题
单选题从具有n个结点的二叉排序树中查找一个元素时,在平均情况下的时间复杂度大致为( )。A
O(n)B
O(1)C
O(log2n)D
O(n2)
热门标签
最新试卷