网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
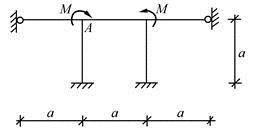
图所示刚架，EI为常数，结点A的转角是（　　）。（提示：利用对称性和转动刚度的概念）



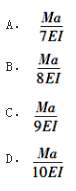
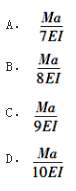
参考答案

参考解析
解析：利用对称性，该结构可以简化为如图示。在A点施加刚臂，转动刚度系数为：k=3i+4i+2i=9i，i=EI/a，转角Z=M/k=Ma/9EI。

更多 “图所示刚架，EI为常数，结点A的转角是（　　）。（提示：利用对称性和转动刚度的概念） ” 相关考题
考题 有如图所示简支梁，其抗弯刚度EI为常数。该梁的挠曲线方程为()。A.B.C.D.
查看答案
考题 图所示刚架，各杆线刚度相同，则结点A的转角大小为（　　）。
查看答案
考题 图所示的刚架，EI＝常数，各杆长为l，A截面的转角为（　　）。
查看答案
考题 如图所示结构，EI为常数，欲使结点B的转角为零，则q的值为（　　）kN/m。 A、0 B、2 C、4 D、8
查看答案
考题 已知刚架的弯矩图如图所示，杆的抗弯刚度为杆的为2EI，则结点B的角位移等于：
查看答案
考题 图示刚架，各杆线刚度相同，则结点A的转角大小为（　　）。
查看答案
考题 图所示刚架，EI=常数，结点A的转角是（　　）。（提示：利用转动刚度的概念）
查看答案
考题 图所示连续梁，EI为常数，用力矩分配法求得结点B的不平衡力矩为（　　）。 A、-20kN·m B、15kN·m C、-5kN·m D、5kN·m
查看答案
考题 图示梁AB，EI为常数，固支端A发生顺时针的支座转动，由此引起的B处的转角为（　　）。
查看答案
考题 图示刚架EI=常数，结点B的水平位移为（　　）。
查看答案
考题 图示刚架，EI=常数，B点的竖向位移(↓)为:
查看答案
考题 图示刚架，EI为常数，结点A的转角是（　　）。（提示：利用对称性和转动刚度的概念）
查看答案
考题 图示刚架EI=常数，截面C和D的相对转角为（　　）。
查看答案
考题 图示刚架，EI为常数，忽略轴向变形。当D支座发生支座沉降时，B点转角为（　　）。
查看答案
考题 图示两刚架的EI均为常数，已知EIa=4EIb，则图a)刚架各截面弯矩与图b)刚架各相应截面弯矩的倍数关系为：
查看答案
考题 图示刚架，EI=常数，结点A的转角是（　　）。（提示：利用转动刚度的概念）
查看答案
考题 图所示梁AB，EI为常数，固支端A发生顺时针的支座转动θ，由此引起的B处的转角为（　　）。 {图} A．θ，顺时针 B．θ，逆时针 C．θ/ 2，顺时针 D．θ/ 2，逆时针
查看答案
考题 图示结构，EI为常数。结点B处弹性支撑刚度系数k=3EI/L3，C点的竖向位移为（　　）。
查看答案
考题 图示为刚架在均布荷载作用下的M图，曲线为二次抛物线，横梁的抗弯刚度为2EI，竖柱为EI，支座A处截面转角为：
查看答案
考题 图式刚架，各杆线刚度i相同，则结点A的转角大小为：
查看答案
考题 用位移法计算图所示梁（EI=常数），基本体系如图所示，k11为（　　）。 A、6EI/l B、7EI/l C、8EI/l D、9EI/l
查看答案
考题 如图a)所示结构，取图b)为力法基本体系，EI=常数，Δ1P为:
查看答案
考题 图示为结构在荷载作用下的M图，各杆EI=常数，则支座B处截面的转角为:
查看答案
考题 用位移法计算图示刚架，画M图。EI=常数。
查看答案
考题 计算图示刚架结点C的水平位移和转角，EI=常数。
查看答案
考题 用位移法求解刚架，并绘弯矩图。各杆EI相同等于常数。
查看答案
考题 关于刚架杆件转动刚度，下列说法中不正确的是（）。A、数值上等于使杆端产生单位转角时需要施加的力矩B、其值仅与杆件的线刚度有关C、远端支承为铰支时其值为3iD、转动刚度表示杆端抵抗转动的能力
查看答案
热门标签
最新试卷