网友您好, 请在下方输入框内输入要搜索的题目:
阅读以下说明和图,填补流程图中的空缺。
【说明】
某汽车制造工厂有两条装配线。汽车装配过程如图10-6所示,即汽车底盘进入装配线,零件在多个工位装配,结束时汽车自动完成下线工作。
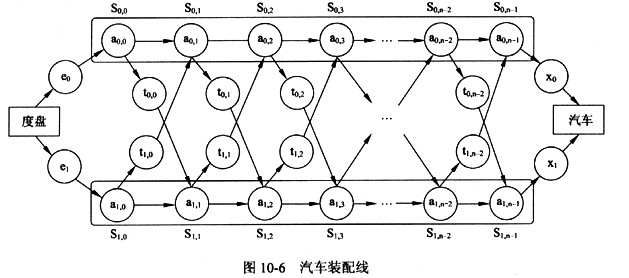
(1)e0和e1表示底盘分别进入装配线0和装配线1所需要的时间。
(2)每条装配线有n个工位,第一条装配线的工位为S0,0,S0,1,…,S0,n-0,第二条装配线的工位为S1,0,S1,1,…,S1,n-1。其中S0,k和S1,k(0≤k≤n-1)完成相同的任务,但所需时间可能不同。
(3)aij表示在工位Sij处的装配时间,其中i表示装配线(i=0或i=1),j表示工位号(0≤j≤n-1)。
(4)tij表示从Sij处装配完成后转移到另一条装配线下一个工位的时间。
(5)X0和X1表示装配结束后,汽车分别从装配线0和装配线1下线所需要的时间。
(6)在同一条装配线上,底盘从一个工位转移到其下一个工位的时间可以忽略不计。
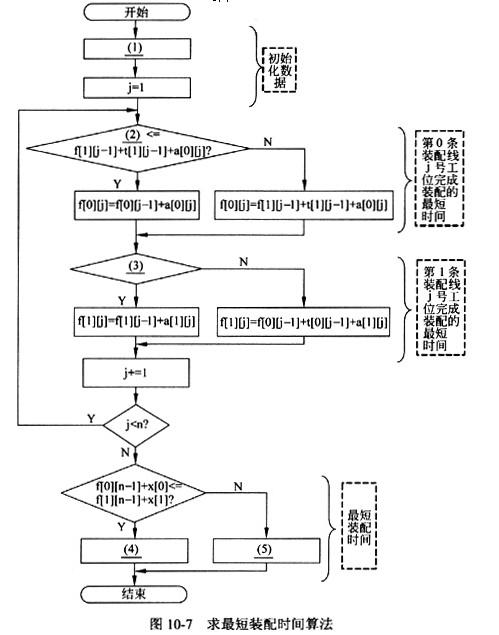
图10-7所示的流程图描述了求最短装配时间的算法,该算法的输入为;
n: 表示装配线上的工位数;
e[i]: 表示e1和e2,i取值为0或1:
a[i][j]: 表示ai,j,i的取值为0或1,j的取值范围为0~n-1;
t[i][j]: 表示ti,j,i的取值为0或1,j的取值范围为0~n-1;
x[i]: 表示X0和X1,i取值为0或1。
算法的输出为:
fi:最短的装配时间;
li:获得最短装配时间的下线装配线号(0或者1)。
算法中使用的f[i][j]表示从开始点到Si,j处的最短装配时间。
参考答案