网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设本金为P,利率为i,本利和为F,计息期数为n,每年末投资为A(在几年内),则现值系数可表示为( )。
A.P(1+i)n
B.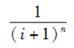
C.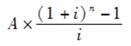
D.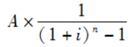
B.
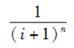
C.
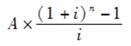
D.
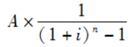
参考答案
参考解析
解析:

更多 “设本金为P,利率为i,本利和为F,计息期数为n,每年末投资为A(在几年内),则现值系数可表示为( )。A.P(1+i)n B. C. D.” 相关考题
考题
若本金为P,年利率为r,每年的计息次数为m次,则n年末该投资的期值计算公式为( )。A.FVn=P(1+r)nB.FVn=P(1+r/n)mnC.FVn=P(1+r/m)mnD.FVn=P(1+r/m)n
考题
以下公式中属于单利计息的是( )。(P 为本金,I 为利息,i 为利率,F 为本利和,n 为计算期)。A.P=I.i.nB.F=P.i.nC.F=P(1+i.n)D.F=P(1+i)n
考题
(2008年)假定现值为P,等额年金为A,年利率为i,那么n年后的本利和F的计算公式为 ( )。A.F=P×(F/P,i,n)B.F=P×(P/F, i,n)C.F=P×(F/A,i,n)D.F=P×(P/A,i,n)
考题
假定现值为P,等额年金为A,年利率为i,那么n年后的本利和F的计算公式为( )。A.F=P×(F/P,i,n)B.F=P×(P/F,i,n)C.F=P×(F/A,i,n)D.F=P×(P/A,i,n)
考题
若以P表示本金,i表示利率,n表示计息期数,I表示利息额,S表示本利和,则单利的计算公式为( )A.S=P(1+n)IB.S=P(1+ni)C.S=Pin(1+ni)D.S=P(1+nI)
考题
设本金为P,利息为I,利率为i,本利和为F,计息期数为n。则以复利计息的本利和计算公式为( )。A.I=P·i·n
B.F=P·i·n
C.F=P(1+i·n)
D.F=P(1+i)n
考题
设本金为P,利息为I,利率为i,本利和为F,计息期数为n。则以复利计息的本利和计算公式为( )。
A.I=P*i*n
B.F=P*i*n
C.F=P(1+i*n)
D.F=P(1+i)n
考题
假设银行利率为i,从现在开始每年年末存款1元,n年后的本利和为(F/A,i,n)元。如果改为每年年初存款,存款期数不变,n年后的本利和应为( )元。A.(F/A,i,n+1)
B.(F/A,i,n+1)-1
C.(F/A,i,n-1)+1
D.(F/A,i,n-1)
考题
假定现值为P,等额年金为A,年利率为i,那么n年后的本利和F的计算公式正确的是()。
A.F=A×(F/P,i,n)
B.F=P×(P/F,i,n)
C.F=A×(F/A,i,n)
D.F=P×(P/A,i,n)
考题
下列有关年金的说法中,正确的是( )。
A. 预付年金终值系数等于普通年金终值系数期数减1,系数加1
B. 预付年金现值系数等于普通年金现值系数期数加1,系数减1
C. 递延期为m,连续等额收到现金流量A的次数为n次,则递延年金现值为P=A×[(P/A,i,n+m)-(P/A,i,m)]
D. 某项年金,从第m期开始,每期期末连续等额收到现金流量A的次数为n次,则递延年金现值为P=A×(P/A,i,n)×(P/F,i,m)
考题
设某项即付年金的期金额为A,折现率为i,计息期数为n,则此即付年金的终值Vn的正确计算公式有()。A、Vn=A(F/A i,n)B、Vn=A(P/A i,n)C、Vn=A(F/A i,n)(1=i)D、Vn=A[(F/A i,n=1)-1]E、Vn=A(P/A i,n)(P/F i,n)
考题
设本金为P,在一年内计息n次,年名义利率为r,实际利率为i,则实际利率与年名义关系为( )。A、i=(1+r/n)n-1B、(1+r/n)nC、(1+n/r)rD、i=(1+n/r)r-1
考题
设某项先付年金的期金额为A,必要的报酬率为i,计息期数为n,则该项先付年金的现值V0的正确计算公式有()A、V0=A(P/Ai,n)B、V0=A(F/Ai,n)C、V0=A(P/Ai,n)(1+i)D、V0=A[(P/Ai,n-1)+1]E、V0=A(P/Ai,n)(P/Fi,n)
考题
单选题若本金为P,年利率为r,每年的计息次数为m,则n年末该投资的终值计算公式为().A
FVn=P(1+r)nB
FVn=P(1+r)mnC
FVn=P(1+r/m)mnD
FVn=P(1+r/m)n
考题
单选题设本金为P,在一年内计息n次,年名义利率为r,实际利率为i,则实际利率与年名义关系为( )。A
i=(1+r/n)n-1B
(1+r/n)nC
(1+n/r)rD
i=(1+n/r)r-1
考题
单选题下列有关年金的有关说法中,正确的是()。A
预付年金终值系数等于普通年金终值系数期数减1,系数加1B
预付年金现值系数等于普通年金现值系数期数加1,系数减1C
递延期为m,连续等额收到现金流量A的次数为n次,则递延年金现值为P=A×[(P/A,i,n+m)-(P/A,i,m)]D
某项年金,从第m期开始,每期期末连续等额收到现金流量A的次数为n次,则递延年金现值为P=A×(P/A,i,n)×(P/F,i,m)
考题
多选题已知从第0年到第n年,每年年值为A,利率为i,期限为n,则现值P为()。AA+A(P/A,i,n)BA(P/A,i,n+1)CA(P/A,i,n+1)(F/P,i,1)DA(F/A,i,n+1)(P/F,i,n)EA(F/A,i,n)(P/F,i,n)
热门标签
最新试卷