网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
某地空调市场被A、B两个品牌占有,每个月的市场占有率分别用An和Bn表示,n=0,1,2,…。据调查,初始时A0=B0=0.5,以后,(An,Bn)=(An-1,Bn-1)M,n=1,2,…,其中M为转移概率矩阵:
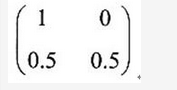
据此,可以推算出,经过一段时间后,这两个品牌的市场占有率将分别趋于( )。
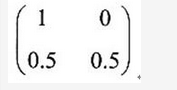
据此,可以推算出,经过一段时间后,这两个品牌的市场占有率将分别趋于( )。
A.0,1
B.0.25,0.75
C.0.75,0.25
D.1,0
B.0.25,0.75
C.0.75,0.25
D.1,0
参考答案
参考解析
解析:本题考查数学(矩阵运算)的应用能力。
根据(An,Bn)=(An-1,Bn-1)M,以及矩阵M的具体数值,可得
An=An-1+0.5Bn-1,Bn=0.5 Bn-1
因此,B1=0.5 B0=0.52,B2=0.5 B1=0.53,…,Bn=0.5n+1→0。
A1=A0+0.5 B0=0.5+0.52,A2=A1+0.5 B1=0.5+0.52+0.53,…,An→1。
从而,(An,Bn)→(1,0)。
根据(An,Bn)=(An-1,Bn-1)M,以及矩阵M的具体数值,可得
An=An-1+0.5Bn-1,Bn=0.5 Bn-1
因此,B1=0.5 B0=0.52,B2=0.5 B1=0.53,…,Bn=0.5n+1→0。
A1=A0+0.5 B0=0.5+0.52,A2=A1+0.5 B1=0.5+0.52+0.53,…,An→1。
从而,(An,Bn)→(1,0)。
更多 “某地空调市场被A、B两个品牌占有,每个月的市场占有率分别用An和Bn表示,n=0,1,2,…。据调查,初始时A0=B0=0.5,以后,(An,Bn)=(An-1,Bn-1)M,n=1,2,…,其中M为转移概率矩阵: 据此,可以推算出,经过一段时间后,这两个品牌的市场占有率将分别趋于( )。A.0,1 B.0.25,0.75 C.0.75,0.25 D.1,0 ” 相关考题
考题
● 众所周知,某类产品的n种品牌在某地区的市场占有率常用向量u=(u1,u2,…,un)表示(各分量分别表示各品牌的市场占有率,各值非负,且总和为1) 。市场占有率每隔一定时间的变化常用转移矩阵Pn*n表示。如果在比较长的一段时期内,转移矩阵的元素均是常数,而当前市场占有率为向量u,则下一时段的市场占有率就是uP,再下一时段的市场占有率就是uP2。假设在某地区,两种冰箱品牌甲与乙当前的市场占有率均为50%,每月市场占有率的变化可用如下常数矩阵来描述:则两个月后,冰箱品牌甲与乙的市场占有率变化情况为 (65) 。(65)A. 甲的市场占有率增加10%,乙的市场占有率减少10%B. 甲的市场占有率减少10%,乙的市场占有率增加10%C. 甲的市场占有率增加14%,乙的市场占有率减少14%D. 甲的市场占有率减少14%,乙的市场占有率增加14%
考题
众所周知,某类产品的n种品牌在某地区的市场占有率常用向量u=(u1,u2,…,un)表示(各分量分别表示各品牌的市场占有率,各值非负,且总和为1)。市场占有率每隔一定时间的变化常用转移矩阵Pn*n表示。如果在比较长的一段时期内,转移矩阵的元素均是常数,而当前市场占有率为向量u,则下一时段的市场占有率就是uP,再下一时段的市场占有率就是uP2。假设在某地区,两种冰箱品牌甲与乙当前的市场占有率均为50%,每月市场占有率的变化可用如下常数矩阵来描述:则两个月后,冰箱品牌甲与乙的市场占有率变化情况为( )。A.甲的市场占有率增加10%,乙的市场占有率减少10%B.甲的市场占有率减少10%,乙的市场占有率增加10%C.甲的市场占有率增加14%,乙的市场占有率减少14%D.甲的市场占有率减少14%,乙的市场占有率增加14%
考题
两个矩阵Am*n和Bn*p相乘,用基本的方法进行,则需要的乘法次数为m*n*p 多个矩阵相乘满足结合律,不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi,M{i+i),…,Mj多个矩阵连乘的最优顺序,即所需要的乘法次数最少。最少乘法次数用m[i,j]表示,其递归式定义为:其中i、j和k为矩阵下标,矩阵序列中Mi的维度为(Pi-i.)*Pi采用自底向上的方法:实现该算法来确定n个矩阵相乘的顺序,其时间复杂度为( 64 )。若四个矩阵M1. M2、M3.,M4相乘的维度序列为2、6、3、10.3,采用上述算法求解,则乘法次数为( 65 )。A.O(N2)B.O(N2Lgn)C.O(N3)D.O(n3lgn)
考题
某类产品n种品牌在某地区的市场占有率常用概率向量u=(u1,u2,…,un)表示(各分量分别表示各品牌的市场占有率,值非负,且总和为1)。市场占有率每隔一定时间的变化常用转移矩阵Pn×n表示。如果在相当长时期内,该转移矩阵的元素均是常数,又设初始时刻的市场占有率为向量u,则下一时刻的市场占有率就是uP,再下一时刻的市场占有率就是uP2,…,而且,市场占有率会逐步稳定到某个概率向量Z,即出现ZP=Z。这种稳定的市场占有率体现了转移矩阵的特征,与初始时刻的市场占有率无关。 假设占领某地区市场的冰箱品牌A与B,每月市场占有率的变化可用如下常数转移矩阵来描述:则冰箱品牌A与B在该地区最终将逐步稳定到市场占有率______。A.(1/4,3/4)B.(1/3,2/3)C.(1/2,1/2)D.(2/3,1/3)
考题
两个矩阵Am*n和Bn*p相乘,用基本的方法进行,则需要的乘法次数为m*n*p。多个矩阵相乘满足结合律,不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi,M(i+1),…,Mj多个矩阵连乘的最优顺序,即所需要的乘法次数最少。最少乘法次数用m[i,j]表示,其递归式定义为:
其中i、j和k为矩阵下标,矩阵序列中Mi的维度为(pi-1)*pi采用自底向上的方法实现该算法来确定n个矩阵相乘的顺序,其时间复杂度为( )A.O(n2)
B.O(n2lgn)
C.O(n3)
D.O(n3lgn)
考题
两个矩阵Am*n和Bn*p相乘,用基本的方法进行,则需要的乘法次数为m*n*p。多个矩阵相乘满足结合律,不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi,M(i+1),…,Mj多个矩阵连乘的最优顺序,即所需要的乘法次数最少。最少乘法次数用m[i,j]表示,其递归式定义为:
其中i、j和k为矩阵下标,矩阵序列中Mi的维度为(pi-1)*pi采用自底向上的方法实现该算法来确定n个矩阵相乘的顺序,若四个矩阵M1、M2、M3、M4相乘的维度序列为2、6、3、10、3,采用上述算法求解,则乘法次数为( )。A.156
B.144
C.180
D.360
考题
在难溶盐的饱和溶液中,各种离子浓度的乘积为一常数,形成沉淀的基本条件是()A、[Am+]n[Bn-]m<KSPB、[Am+]n[Bn-]m>KSPC、[Am+]n[Bn-]m≤KSPD、[Am+]n[Bn-]m=KSP
考题
对于一难溶电解质AnBm(S)nAm++mBn-要使沉淀从溶液中析出,则必须()。A、[Am+]n[Bn-]m=KspB、[Am+]n[n-]m〉KspC、[Am+]n[Bn-]m〈KspD、[Am+1]〉[Bn-1]
考题
单选题大偏心受压构件的承载力随着M和N的变化也将变化,下列论述正确的是()。A
M不变时,N越小越危险B
N不变时,M越小越危险C
M不变时,N越大越危险D
M不变时,N越小越危险和N不变时,M越小越危险
考题
单选题对一难溶电解质AnBm(S)nAm++mBn-要使沉淀从溶液中析出,则必须()。A
[Am+]n[Bn-]m=KSPB
[Am+]n[Bn-]mKSPC
[Am+]n[Bn]mKSPD
[Am+1][Bn-1]
考题
单选题宫颈癌,左侧宫旁可触及一孤立性的固定肿块,按UICC分期为( )A
T2bN1M0B
T2aN2M0C
T2bN2M0D
T3N1M0E
T3N2M0
热门标签
最新试卷