网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
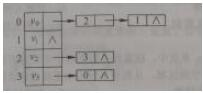
某有向图G的邻接表如下图所示,可看出该图中存在弧,而不存在从顶点v.出发的弧。以下关于图G的叙述中,错误的是( )

A.G中存在回路
B.G中每个顶点的入度都为1
C.G的邻接矩阵是对称的
D.不存在弧小于V3,vi>
B.G中每个顶点的入度都为1
C.G的邻接矩阵是对称的
D.不存在弧小于V3,vi>
参考答案
参考解析
解析:
更多 “某有向图G的邻接表如下图所示,可看出该图中存在弧,而不存在从顶点v.出发的弧。以下关于图G的叙述中,错误的是( ) A.G中存在回路 B.G中每个顶点的入度都为1 C.G的邻接矩阵是对称的 D.不存在弧小于V3,vi>” 相关考题
考题
● 若无向连通图 G 具有 n个顶点,则以下关于图 G的叙述中,错误的是(43)。(43)A.G 的边数一定多于顶点数B.G 的生成树中一定包含 n个顶点C.从 G 中任意顶点出发一定能遍历图中所有顶点D.G 的邻接矩阵一定是n阶对称矩阵
考题
阅读下列说明和C代码,回答问题1至问题3,将解答写在答题纸的对应栏内。【说明】对有向图进行拓扑排序的方法是:(1)初始时拓扑序列为空;(2)任意选择一个入度为0的顶点,将其放入拓扑序列中,同时从图中删除该顶点以及从该顶点出发的弧;(3)重复(2),直到不存在入度为0的顶点为止(若所有顶点都进入拓扑序列则完成拓扑排序,否则由于有向图中存在回路无法完成拓扑排序)。函数int*TopSort(LinkedDigraph G)的功能是对有向图G中的顶点进行拓扑排序,返回拓扑序列中的顶点编号序列,若不能完成拓扑排序,则返回空指针。其中,图G中的顶点从1开始依次编号,顶点序列为vl,v2,…,vn,图G采用邻接表表示,其数据类型定义如下:define MAXVNUM 50 /*最大顶点数*/typedef struct ArcNode| /*表结点类型*/int adjvex; /*邻接顶点编号*/struct ArcNode*nextarc; /*指示下一个邻接顶点*/{ArcNode;typedef struct AdjList{ /*头结点类型*/char vdata; /*顶点的数据信息*/ArcNode*firstarc; /*指向邻接表的第一个表结点*/}AdjList;typedef struct LinkedDigraph /*图的类型*/int n: /*图中顶点个数*/AdjList Vhead[MAXVNUM]; /*所有顶点的头结点数组*/}LinkedDigraph;例如,某有向图G如图4-1所示,其邻接表如图4-2所示。函数TopSort中用到了队列结构(Queue的定义省略),实现队列基本操作的函数原型如下表所示:【C代码】int*TopSort(LinkedDigraph G){ArcNode*P; /*临时指针,指示表结点*/Queue Q; /*临时队列,保存入度为0的顸点编号*/int k=0; /*临时变量,用作数组元素的下标*/int j=0,w=0; /*临时变量,用作顶点编号*/int*topOrder,*inDegree;topOrder=(int*)malloc((G.n+1)*sizeof(int));/*存储拓扑序列中的顶点编号*/inDegree=(int*)malloc((G.n+1)*sizeof(int));/*存储图G中各顶点的入度*/if(!inDegree||!topOrder) return NULL;(1); /*构造一个空队列*/for(j=1;j=Gn;j++){ /*初始化*/topOrder[j]=0;inDegree[j]=0;}for(j=1;j=Gn;j++) /*求图G中各顶点的入度*/for(p=G.Vhead[j].firstarc;p;p=p-nextarc)inDegree[P-adjvex]+=1;for(j=i;j=G.n;J++) /*将图G中入度为0的顶点保存在队列中*/if(0==inDegree[j]) EnQueue(Q,j);while(! IsEmpty(Q)){(2); /*队头顶点出队列并用w保存该顶点的编号*/topOrder[k++]=w; /*将顶点W的所有邻接顶点的入度减l(模拟删除顶点w及该顶点出发的弧的操作)*/for(p=G.Vhead[w].firstarc;p;p=p-nextarc){(3)-=1;if(0== (4) ) EnQueue(Q,P-adjvex);}/*for*/}/ * while*/free(inDegree);if( (5) )return NULL;return topOrder;}/*TopSort*/根据以上说明和C代码,填充C代码中的空(1)
考题
设某有向无环图的顶点个数为n、弧数为e,那么用邻接表存储该图时,实现上述拓扑排序算法的函数TopSort的时间复杂度是(6)。若有向图采用邻接矩阵表示(例如,图4-1所示有向图的邻接矩阵如图4-3所示),且将函数TopSort中有关邻接表的操作修改为针对邻接矩阵的操作,那么对于有n个顶点、e条弧的有向无环图,实现上述拓扑排序算法的时问复杂度是(7)。
考题
若无向连通图G具有n个顶点,则以下关于图G的叙述中,错误的是( )。A.c的边数一定多于顶点数B.G的生成树中一定包含n个顶点C.从c中任意顶点出发一定能遍历图中所有顶点D.G的邻接矩阵一定是n阶对称矩阵
考题
阅读以下函数说明和C代码,将C程序中(1)~(5)空缺处的语句填写完整。[说明]函数int Toplogical(LinkedWDigraphG)的功能是对图G中的顶点进行拓扑排序,并返回关键路径的长度。其中,图G表示一个具有n个顶点的AOE-网,图中顶点从1~n依次编号,图G的存储结构采用邻接表表示,其数据类型定义如下。例如,某AOE-网如图6-22所示,其邻接表存储结构如图6-23所示。[函数]
考题
在一个有向图G的拓扑序列中,顶点Vi排列在Vj之前,说明图G中(59)。A.一定存在弧B.
在一个有向图G的拓扑序列中,顶点Vi排列在Vj之前,说明图G中(59)。A.一定存在弧<vi,vj>B.一定存在弧<vj,vi>C.可能存在vi到vj的路径,而不可能存在vj到vi的路径D.可能存在vj到vi的路径,而不可能存在vi到vj的路径
考题
对于连通无向图G,以下叙述中,错误的是( )。A. G 中任意两个顶点之间存在路径 B. G 中任意两个顶点之间都有边 C. 从 G 中任意顶点出发可遍历图中所有顶点 D. G的邻接矩阵是对称的
考题
某有向图 G 及其邻接矩阵如下所示。以下关于图的邻接矩阵存储的叙述中,错误的是( )。A. 有向图的邻接矩阵可以是对称矩阵B. 第 i行的非零元素个数为顶点 i的出度C. 第 i行的非零元素个数为顶点 i的入度D. 有向图的邻接矩阵中非零元素个数为图中弧的数目
考题
阅读以下说明和代码,填补代码中的空缺,将解答填入答题纸的对应栏内。 【说明】 图是很多领域中的数据模型,遍历是图的一种基本运算。从图中某顶点v出发进行广度优先遍历的过程是: ①访问顶点v; ②访问V的所有未被访问的邻接顶点W1 ,W2 ,..,Wk; ③依次从这些邻接顶点W1 ,W2 ,..,Wk出发,访问其所有未被访问的邻接顶点;依此类推,直到图中所有访问过的顶点的邻接顶点都得到访问。 显然,上述过程可以访问到从顶点V出发且有路径可达的所有顶点。对于从v出发不可达的顶点u,可从顶点u出发再次重复以上过程,直到图中所有顶点都被访问到。 例如,对于图4-1所示的有向图G,从a出发进行广度优先遍历,访问顶点的一种顺序为a、b、c、e、f、d。设图G采用数组表示法(即用邻接矩阵arcs存储),元素arcs[i][j]定义如下:图4-1的邻接矩阵如图4-2所示,顶点a~f对应的编号依次为0~5.因此,访问顶点a的邻接顶点的顺序为b,c,e。 函数BFSTraverse(Graph G)利用队列实现图G的广度优先遍历。 相关的符号和类型定义如下: define MaxN 50 /*图中最多顶点数*/ typedef int AdjMatrix[MaxN][MaxN]; typedef struct{ int vexnum, edgenum; /*图中实际顶点数和边(弧)数*/ AdjMatrix arcs; /*邻接矩阵*/ )Graph; typedef int QElemType; enum {ERROR=0;OK=1}; 代码中用到的队列运算的函数原型如表4-1所述,队列类型名为QUEUE。 表4-1 实现队列运算的函数原型及说明【代码】 int BFSTraverse(Graph G) {//对图G进行广度优先遍历,图采用邻接矩阵存储 unsigned char*visited; //visited[]用于存储图G中各顶点的访问标志,0表示未访问 int v, w, u; QUEUEQ Q; ∥申请存储顶点访问标志的空间,成功时将所申请空间初始化为0 visited=(char*)calloc(G.vexnum, sizeof(char)); If( (1) ) retum ERROR; (2) ; //初始化Q为空队列 for( v=0; vG.vexnum; v++){ if(!visited[v]){ //从顶点v出发进行广度优先遍历 printf(%d,v); //访问顶点v并将其加入队列 visited[v]=1; (3) ; while(!isEmpty(Q)){ (4) ; //出队列并用u表示出队的元素 for(w=0;vG.vexnum; w++){ if(G.arcs[u][w]!=0 (5) ){ //w是u的邻接顶点且未访问过 printf(%d, w); //访问顶点w visited[w]=1; EnQueue(Q, w); } } } } free(visited); return OK; )//BFSTraverse
考题
拓扑序列是有向无环图中所有顶点的一个线性序列,若有向图中存在弧或存在从顶点v到w的路径,则在该有向图的任一拓扑序列中,V一定在w之前。下面有向图的拓扑序列是( )A.41235B.43125C.42135D.41=325
考题
对于连通无向图 G,以下叙述守,错误的是(43)A.G 中任意两个顶点之间存在路径
B.G 中任意两个顶点之间都有边
C.从 G 中任意顶点出发可遍历图中所有顶点
D.G 的邻接矩阵是对称的
考题
某有向图G的邻接表如下图所示,可看出该图中存在弧,而不存在从顶点Vi出发的弧。关于图G的叙述中,错误的是()。
A.G中存在回路
B.G中每个顶点的入度都为1
C.G的邻接矩阵是对称的
D.G中不存在弧瓜
考题
拓扑序列是有向无环图中所有顶点的一个线性序列,若有向图中存在弧或存在从顶点v到w的路径,则在该有向图的任一拓扑序列中,v一定在w之前。下面有向图的拓扑序列是( )。
A.41235
B.43125
C.42135
D.41325
考题
以下关于无向连通图 G 的叙述中,不正确的是(60)。A.G 中任意两个顶点之间均有边存在
B.G 中任意两个顶点之间存在路径
C.从 G 中任意顶点出发可遍历图中所有顶点
D.G 的临接矩阵是对称矩阵
考题
填空题若在有向图G中存在一条弧i,Vj,则称顶点Vj()于顶点Vi。
热门标签
最新试卷