网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
设有三元方程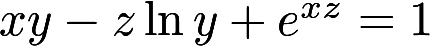
，根据隐函数存在定理，存在点(0,1,1)的一个邻域，在此邻域内该方程
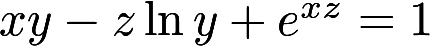，根据隐函数存在定理，存在点(0,1,1)的一个邻域，在此邻域内该方程A.只能确定一个具有连续偏导数的隐函数z=z(x,y)
B.可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y)
C.可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y)
D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)
B.可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y)
C.可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y)
D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)
参考答案
参考解析
解析：
更多 “设有三元方程 ，根据隐函数存在定理，存在点(0,1,1)的一个邻域，在此邻域内该方程A.只能确定一个具有连续偏导数的隐函数z=z(x,y) B.可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y) C.可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y) D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)” 相关考题
考题
设函数f(x)在x=a的某个邻域内连续，且f(a)为其极大值，则存在δ＞0，当x∈(a-δ，a+δ)时，必有( )。A.(x-a)[f(x)-f(a)]≥0
B.(x-a)[f(x)-f(a)]≤0
C.
D.
考题
设y=f(x)是微分方程y-2y+4y=0的一个解，又f(xo)＞0，f(xo)=0，则函数f(x)在点xo( ).A.取得极大值
B.取得极小值
C.的某个邻域内单调增加
D.的某个邻域内单调减少
考题
A. x=0是f(x)的极小值点
B.x=0是f(x)的极大值点
C. 曲线y=f(x)在点（0,f（0））的左侧邻域是凹的，右侧邻域是凸的
D.曲线y=f(x)在点（0,f（0））的左侧邻域是凸的，右侧邻域是凹的
考题
高中“方程的根与函数的零点”(第一节课)设定的教学目标如下：
①通过对二次函数图象的描绘，了解函数零点的概念，渗透由具体到抽象思想，领会函数零点与相应方程实数根之间的关系；
②理解提出零点概念的作用，沟通函数与方程的关系。
③通过对现实问题的分析，体会用函数系统的角度去思考方程的思想，使学生理解动与静的辨证关系。掌握函数零点存在性的判断。完成下列任务：
(1)根据教学目标，设计一个问题引入，并说明设计意图；
(2)根据教学目标①，设计问题链(至少包含三个问题)，并说明设计意图；
(3)根据教学目标③，给出至少一个实例和三个问题，并说明设计意图；
(4)确定本节课的教学重点；
(5)作为高中阶段的基础内容，其难点是什么
(6)本节课的教学内容对后续哪些内容的学习有直接影响
考题
下列说法中正确的是（）A、几个简单的势流之所以能通过简单的叠加得到一个复杂的势流，是因为势流的速度势函数是线性函数B、几个简单的势流之所以能通过简单的叠加得到一个复杂的势流，是因为势流的基本方程——拉普拉斯方程是线性齐次方程C、无环量圆柱绕流是由直线等速流与点源叠加而成的D、流函数存在的充分必要条件是满足连续性方程，即对于连续的平面运动，流函数总是存在的
考题
设y=f（x）是微分方程y"-2y’+4y=0的一个解，又f（x0）O，f’（x0）=0，则函数f（x）在点x0（）．A、取得极大值B、取得极小值C、的某个邻域内单调增加D、的某个邻域内单调减少
考题
以下说法正确的是（）A、库塔-茹可夫斯基定理对流体具有普适性。B、如果流动存在势函数，则也存在流函数。C、涡量输运方程表明破坏旋涡守恒的根源是粘性作用。D、流层之间的内摩擦力与接触面上的压力无关。
考题
单选题设y=f（x）是微分方程y"-2y’+4y=0的一个解，又f（x0）O，f’（x0）=0，则函数f（x）在点x0（）．A
取得极大值B
取得极小值C
的某个邻域内单调增加D
的某个邻域内单调减少
考题
单选题设确定了函数y＝g（x），则（ ）。A
x＝0是函数y＝g（x）的驻点，且是极大值点B
x＝0是函数y＝g（x）的驻点，且是极小值点C
x＝0不是函数y＝g（x）的驻点D
存在x＝0的一个小邻域，y＝g（x）是单调的
考题
单选题设y＝f（x）是y″－2y′＋4y＝0的一个解，若f（x0）＞0且f′（x0）＝0，则f（x）在点x0处（ ）。A
取得极大值B
某邻域内单调递增C
某邻域内单调递减D
取得极小值
考题
单选题设y=f（x）是满足微分方程y″+y′-esinx=0的解，且f′（x0）=0，则f（x）在（ ）。A
x0的某个邻域内单调增加B
x0的某个邻域内单调减少C
x0处取得极小值D
x0处取得极大值
考题
单选题y＝f（x）是方程y″－2y′＋4y＝0的一个解，若f（x0）＞0，f′（x0）＝0，则函数f（x）（ ）。A
在x0点取得极大值B
在x0的某邻域单调增加C
在x0点取得极小值D
在x0的某邻域单调减少
考题
单选题设三元函数xy－zlny＋exz＝1，根据隐函数存在定理，存在点（0，1，1）的一个邻域，在此邻域内该方程（ ）。A
只能确定一个具有连续偏导数的隐函数z＝z（x，y）B
可确定两个具有连续偏导数的隐函数y＝y（x，z）和z＝z（x，y）C
可确定两个具有连续偏导数的隐函数x＝x（y，z）和z＝z（x，y）D
可确定两个具有连续偏导数的隐函数x＝x（y，z）和y＝y（x，z）
考题
多选题下列说法中正确的是（）A几个简单的势流之所以能通过简单的叠加得到一个复杂的势流，是因为势流的速度势函数是线性函数B几个简单的势流之所以能通过简单的叠加得到一个复杂的势流，是因为势流的基本方程——拉普拉斯方程是线性齐次方程C无环量圆柱绕流是由直线等速流与点源叠加而成的D流函数存在的充分必要条件是满足连续性方程，即对于连续的平面运动，流函数总是存在的
热门标签
最新试卷
