贵州省:震惊!2020年公用设备工程师案例分析题居然还能这么答?!
发布时间:2020-01-30
常言道:天道酬勤。曾经的每一份付出,必将收到百倍回报,不管揭晓的答案是什么,只要努力过、奋斗过,就不要后悔。虽然我们还不知道今年公用设备师考试什么时候报名,但是我们可以根据2019年的考试报名时间预计得出今年的考试报名将于8月份进行。另外,关于注册公用设备工程师考试考前应该如何规划的那些事儿你了解吗?不了解就赶紧来看看下面的案例分析题题型解答方法吧:
一、难题跳过法(即是答题要做到先易后难,把自己较为熟悉的、较为容易的题目都做上,再去考虑不太熟悉、不太容易的、或计算量较大的难题)
以牛人的经验来看,考案例分析,就是采用围追堵截的办法,把较为容易的、较为熟悉的题目都做上,然后攻击不太熟悉、不太容易的、或计算量较大的难题,最低要求就是利用3个小时,至少要答上18道题目,然后争取拿下20道,在比较有把握的情况下,剩余时间较为充足的情况下,再冲击25道。
这其实和奥运会举重比赛是一样的道理,开把要成绩(18道,容错率只有3道,其中2道左右是陷阱,1道失误,需要有极高的把握能力,且火眼金睛般地迅速识破陷阱), 二把上水平(20道,容错率放宽至5道,这时候考生可能心里比较有底了,从而产生松泄情绪或自满情绪,从而易被陷阱迷惑你的双眼而出乎意料地做错许多道题目而功亏一篑),三把靠发挥(25道,你都能做满25道了,如果还没通过那一定是犯了-4哥的错误!)。
二、考试注意力高度集中(即是平时准备比较充分,考试注意力高度集中)
平时准备比较充分,考试注意力高度集中,保证能够答上18道题目,但其实通过率一点都不比答20道甚至答满25道题目低,因为在注意力高度集中的情况下,答错的几率很低,18道题目,平均每道题目也只有10分钟的时间,这10分钟内,你除了要做答外,还要包括审题,尤其是要识别是否有陷阱,所以时间并不很充裕,但是如果你要去做20道,甚至冲击25道,那时间就更加不充裕了,出错的概率极大,因此,考场上要摆正心态,千万别总想要冲击25道题目。
牛人的理解是,如果能轻易让你答满25道题目,那出题的人就别干了,赶紧回家该干嘛干嘛去。总共 30道题目,即使你复习再好,复习再充分,水平再高,也总有那么十几道是你不熟悉或你比较容易进坑的题目。你们复习的时候肯定要琢磨题目能在哪儿出,以什么形式出现等等,那出题的人也同样要与你们在斗心眼儿,肯定会挖空心思地要琢磨你们的心理,并且尽量地反其道而行之,最终的通过率也就是15-25%的水平,即使你通过了,分数不会太高的,普遍是60-70的水平,虽然2011年有这样的情况,但那纯属特例,以后我估计不会再有这种情况了。所以,还是那句话,25道题目,做答完全且正确的,那纯是给神仙一般的人准备的,普通考生们还是先60分万岁,然后再在60分万岁的基础上尽量提高分数吧。
三、通读所有题目,不要盲目做难题(当你看完所有的题目时就要对题目做个取舍,哪些你能做上并且可以保证正确率,哪些你不能保证)
所以说,上、下午各能做得上18道题目,已经有很大可能成绩 达到合格标准了,在没有把握的前提下,还是应该重点要检查那做出来的18道题目,不要盲目多做那些你不太熟悉或没啥把握的题目,因为那样可能会导致你做得上的那18道题中出现失误,当然,如果答出的题目不足 18道,甚至连15道都没有的情况下,也别放弃,你还有第二场比赛的机会,届时要靠充分发挥,争取总成绩过合格标准!
四、合理分配考试时间(这是考试中最重要的一条,考试时不要在某道题目耗费大量时间,要学会战术放弃!)
千万要记住,合理分配考试时间是至关重要,不要在某道题目耗费大量时间,要学会战术放弃!
最后再叮嘱一句:除了要仔细涂卡,卷子上的答题时候,一定要把答案字母填在括号内,别再划勾了,否则得了-4分是很可惜的,心情全年都不一定能淡定下来的。
看完上面的案例分析题题型解答之后,相信很多小伙伴都跃跃欲试了吧,但是现在还是好好备考吧。想知道准考证打印时间是什么时候吗?然而今年的相关文件并未下发,但是根据2019年公用设备工程师考试准考证打印工作于10月份开始,我们可以预计得出2020年准考证打印时间也将于10月初考试前的一到两个周进行。我知道,你们已经为自己设计好了一幅美好的蓝图,并且你们也正在为实现这一目标努力奋斗着。我相信各位考生一定能成功。祝愿你们,美好的明天属于不断进取的攀登者!
下面小编为大家准备了 公用设备师 的相关考题,供大家学习参考。
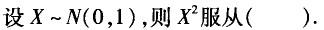
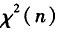
B.
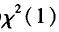
C.t(1)
D.N(0,1)
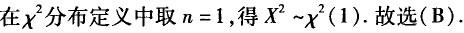
B.n-1
C.1/n
D.(n+1)/n
B.p<q
C.p=q
D.不能确定
声明:本文内容由互联网用户自发贡献自行上传,本网站不拥有所有权,未作人工编辑处理,也不承担相关法律责任。如果您发现有涉嫌版权的内容,欢迎发送邮件至:contact@51tk.com 进行举报,并提供相关证据,工作人员会在5个工作日内联系你,一经查实,本站将立刻删除涉嫌侵权内容。
- 2020-01-29
- 2019-08-03
- 2019-07-21
- 2020-01-30
- 2019-07-21
- 2019-07-21
- 2020-01-29
- 2019-12-29
- 2019-07-21
- 2020-01-30
- 2019-07-21
- 2019-07-21
- 2019-07-21
- 2019-07-21
- 2020-01-30
- 2019-07-21
- 2020-01-30
- 2019-12-29
- 2019-07-21
- 2019-07-21
- 2020-01-29
- 2020-01-29
- 2020-01-29
- 2021-04-18
- 2019-07-21
- 2020-01-29
- 2020-01-29
- 2019-07-21
- 2020-01-29
- 2020-01-03