2021年电气工程师《基础知识》模拟试题(2021-02-03)
发布时间:2021-02-03
2021年电气工程师《基础知识》考试共题,分为。小编为您整理精选模拟习题10道,附答案解析,供您考前自测提升!
1、设齐次线性方程组 有非零解,则等于:()。 【单选题】
A.-1
B.0
C.1
D.2
正确答案:A
答案解析:由题意得:则入=-1。主要考点:齐次线性方程组有非零解的条件。
2、某公司准备建立一项为期10年的奖励基金,用于奖励有突出贡献的员工,每年计划颁发10万元奖金,从第1年开始至第10年正好用完账户中的所有款项,若利率为6%,则第1年初存入的奖励基金应为多少元: 【单选题】
A.1318079
B.1243471
C.780169
D.736009
正确答案:D
答案解析:根据等额分付现值公式,
3、根据《建设工程勘测设计管理条例》的规定,编辑初步设计文件应当: .【单选题】
A.满足编制方案设计文件和控制概算的需要
B.满足编制施工招标文件,主要设备材料订货和编制施工图设计文件的需要
C.满足非标准设备制作,并注明建筑工程合理使用年限
D.满足设备材料采购和施工的需要
正确答案:B
答案解析:编辑初步设计文件应当满足编制施工招标文件,主要设备材料订货和编制施工图设计文件的需要。
4、在铜锌原电池中,将铜电极的则铜电极的电极电势:()。【单选题】
A.变大
B.变小
C.无变化
D.无法确定
正确答案:C
答案解析:铜电极的电离为铜电极的电极电势为可见铜电极的电极电势与无关,所以铜电极的电极电势不变,故应选C。 主要考点:电极电势的影响因素及应用。
5、弹簧一物块直线振动系统位于铅垂面内。弹簧刚度系数为k,物块质量为m。若已知物块的运动微分方程为 kx= 0,则描述运动的坐标Ox的坐标原点应为:【单选题】
A.弹簧悬挂处之点
B.弹簧原长处之点
C.弹簧由物块重力引起静伸长之点
D.任意点皆可
正确答案:C
答案解析:这题是考察坐标系坐标原点的选取,此题复杂点在弹簧,应选受力平衡点,即加速度为0时的点为坐标原点,质点的位移方程为:,可知,当x=0时,加速度为0,即合力为0,在点处符合。
6、确定原子轨道函数ψ形状的量子数是:()。【单选题】
A.主量子数
B.角量子数
C.磁量子数
D.自旋量子数
正确答案:B
答案解析:根据量子数的含义,角量子数确定原子轨道形状。
7、在固定的坐标系Oxyz中, 长方体作平移(或称平动)。长方体的自由度数为:【单选题】
A.1个
B.2个
C.3个
D.4个
正确答案:C
答案解析:平动,三个方向能动,则自由度为3。
8、梯形断面水渠按均匀流设计,已知过水断面A=5.04 ,湿周x=6.73m, 粗糙系数n=0.025,按曼宁公式计算谢才系数C为:【单选题】
A.30.80/s
B.30.13 /s
C.38.80/s
D.38.13/s
正确答案:D
答案解析:水力半径:,谢才系数:。
9、新设法人融资方式,建设项目所需要资金来源于: ()【单选题】
A.资本金和权益资金
B.资本金和注册资本
C.资本金和债务资金
D.建设资金和债务资金
正确答案:C
答案解析:新设法人的融资,按融资的性质可以分为权益融资和债务融资。权益融资形成项目的资本金;债务融资形成项目的债务资金。
10、微分方程满足初始条件的特解是:()。 【单选题】
A.
B.
C.,c为任意常数
D.
正确答案:A
答案解析:这是一阶线性非齐次微分方程,
下面小编为大家准备了 电气工程师 的相关考题,供大家学习参考。

A. tanf≤θ B. tanf>θ C. tanθ≤f D. tanθ>f

B.1
C.2
D.不存在


B.
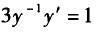
C.y´=3y+1
D.

声明:本文内容由互联网用户自发贡献自行上传,本网站不拥有所有权,未作人工编辑处理,也不承担相关法律责任。如果您发现有涉嫌版权的内容,欢迎发送邮件至:contact@51tk.com 进行举报,并提供相关证据,工作人员会在5个工作日内联系你,一经查实,本站将立刻删除涉嫌侵权内容。
- 2020-12-04
- 2021-08-05
- 2020-08-31
- 2020-09-17
- 2020-04-01
- 2020-12-21
- 2020-09-07
- 2021-03-04
- 2021-09-05
- 2021-01-02
- 2021-06-30
- 2021-01-25
- 2021-08-02
- 2020-09-10
- 2020-07-03
- 2020-09-14
- 2021-05-30
- 2020-09-28
- 2020-05-11
- 2020-10-24
- 2020-06-22
- 2020-12-23
- 2020-08-23
- 2021-02-25
- 2021-08-21
- 2021-02-19
- 2021-01-23
- 2019-03-02
- 2021-03-19
- 2021-07-12