2021年电气工程师《供配电专业》历年真题(2021-09-23)
发布时间:2021-09-23
2021年电气工程师《供配电专业》考试共题,分为。小编为您整理历年真题10道,附答案解析,供您考前自测提升!
1、已知平面简谐波的方程为:y = Acos(Bt-Cx)式中A、B、C为正常数,此波的波长和波速分別为()。【单选题】
A.
B.
C.
D.
正确答案:B
答案解析:此题考查波动方程基本关系。
2、用电压表测量图示电路的结果是10V和0. 2A,设电流的初相位为10°,电压与电流呈反相关系,则如下关系成立的是()。 【单选题】
A.
B.
C.
D.
正确答案:D
答案解析:画相量图分析(见解图),电压表和电流表读数为有效值。
3、设二维随机变量(X,Y)的概率密度为,则常数a,b应满足的条件是()。【单选题】
A.ab=-1/2,且a>0,b<0
B.ab=1/2,且a>0,b>0
C.ab=-1/2,a0
D.ab=1/2,且 a<0,b<0
正确答案:A
答案解析:本题考查概率密度的性质:方法1:当a>0 时,当 b方法 2:当x>0,y>0时,当时,x与y相互独立。X服从参数λ=2a(a>0)的指数分布,Y服从参数λ= -b(b
4、函数f(x,y)在点处有一阶偏导数是函数在该点连续的()。【单选题】
A.必要条件
B.充分条件
C.充分必要条件
D.既非充分又非必要
正确答案:D
答案解析:本题考查多元函数微分学的概念性问题,涉及多元函数偏导致与多元函数连续等概念,需记忆下图的关系式方可快速解答:f(x,y)在点有一阶偏导数,不能推出f(x,y)在连续。同样,f(x,y)在连续,不能推出f(x,y)在有一阶偏导数。可知,函数可偏导与函数连续之间的关系是不能相互导出的。
5、函数在区间[-π,π]上的最小位点等于()。【单选题】
A.-π
B.0
C.π/2
D.π
正确答案:B
答案解析:本题考查了三角函数的基本性质,可以采用求导的方法直接求出。方法 1: x∈[-π,π]f\'(x)= sinx,f\'(x)=0,即sinx=0,x=0,-π,π为驻点则 f(0)=-cos0 =-1,f(-π)=- cos(-π) = 1,f(π)-cos(π) = 1所以x= 0,函数取得故小值,最小值点。方法2:通过作图,可以看出在[-π,π]上的最小值点。
6、曲线的拐点是()。【单选题】
A.
B.
C.(-1,e)
D.
正确答案:A
答案解析:本题考查函数拐点的求法。求解函数拐点即求函数的二阶导数为0的点,因此有:令f”(x)=0,解出x=2当x∈€(-∞,2)时,f”(x)当x∈€(2,+∞)时,f”(x)>0所以拐点为
7、某产品共有五项功能,用强制确定法确定零件功能评价体系时,其功能得分分别为3、5、4、1、2,则的功能评价系数为()。【单选题】
A.0. 20
B.0. 13
C.0. 27
D.0. 33
正确答案:C
答案解析:的功能系数为:。
8、设为三阶实对称矩阵A的特征值,属于的特征向量为 ,则属于的特征向量是()。【单选题】
A.
B.
C.
D.
正确答案:A
答案解析:本题考查特征值与特征向量的相关计算性质。已知重要结论:实对称矩阵属于不同特征值的特征向量必然正交。方法1:设对应的特征向量,由于A是实对称矩阵,故,即该同解方程组为当方程组的基础解系方法2:采用代入法,对四个选项进行验证,对于选项A:,可知正确。
9、杆OA=l,绕固定轴O转动,某瞬时杆端A点的加速度a如图所示,则该瞬时杆OA的角速度及角加速度为()。【单选题】
A.
B.
C.
D.
正确答案:C
答案解析:根据定轴转动刚体上一点加速度与转动角速度、角加速度的关系:,,而题中。
10、在双缝干涉实验中,入射光的波长为λ,用透明玻璃纸遮住双缝中的一条缝(靠近屏的一侧),若玻璃纸中光程比相同厚度的空气的光程大2. 5λ,则屏上原来的明 纹处()。【单选题】
A.仍为明条纹
B.变为暗条纹
C.既非明条纹也非暗条纹
D.无法确定是明纹还是暗纹
正确答案:B
答案解析:光的干涉,光程差变化为半波长的奇数倍时,原明纹处变为暗条纹。
下面小编为大家准备了 电气工程师 的相关考题,供大家学习参考。
B. 功率角增大,功率因数减小
C. 功率角减小,功率因数增大
D. 功率角增大,功率因数增大

A.熔断器; B.连接片;
C.不需要拆除导线的特殊端子; D.半导体电器。
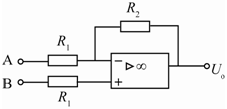
B、 -8V
C、 10V
D、 -10V

A.1.05; B.1.08; C.1.10; D.1.12。
声明:本文内容由互联网用户自发贡献自行上传,本网站不拥有所有权,未作人工编辑处理,也不承担相关法律责任。如果您发现有涉嫌版权的内容,欢迎发送邮件至:contact@51tk.com 进行举报,并提供相关证据,工作人员会在5个工作日内联系你,一经查实,本站将立刻删除涉嫌侵权内容。
- 2021-10-04
- 2020-12-28
- 2021-10-17
- 2021-07-02
- 2022-01-14
- 2022-05-12
- 2021-04-03
- 2022-03-11
- 2022-01-31
- 2020-10-27
- 2021-03-19
- 2021-03-14
- 2022-02-16
- 2021-06-29
- 2020-12-11
- 2021-06-02
- 2020-12-06
- 2021-09-10
- 2022-02-11
- 2022-01-29
- 2022-02-07
- 2021-05-23
- 2020-08-26
- 2021-07-01
- 2022-01-23
- 2020-09-04
- 2020-10-07
- 2021-01-04
- 2020-11-11
- 2021-06-22