2020年电气工程师《供配电专业》历年真题(2020-12-21)
发布时间:2020-12-21
2020年电气工程师《供配电专业》考试共题,分为。小编为您整理历年真题10道,附答案解析,供您考前自测提升!
1、已知交流电流i(t)的周期T=1m,有效值I= 0. 5A,当t= 0时,,则它的时间函数描述形式是()。【单选题】
A.
B.i(t)=0. 5sin2000πtA
C.
D.
正确答案:C
答案解析:
2、等截面杆,轴向受力如图所示,则杆的最大轴力是()。【单选题】
A.8kN
B.5kN
C.3kN
D.13kN
正确答案:B
答案解析:用直接法求轴力,可得:左段杆的轴力是-3kN,右段杆的轴力是5kN。所以杆的最大轴力是5kN。
3、29. 一平面简谐波的波动方程为y=0.01cos10π(25t-x) (SI),则在t = 0. 1s时刻,x = 2m处质元的振动位移是()。【单选题】
A.0.01cm
B.0.01m
C.-0.01m
D.0.01mm
正确答案:C
答案解析:将t=0.1s,x=2m代入方程,即y=0.01cos10π(25t-x) =0. 01cos10π (2. 5- 2) = -0. 01
4、图示电路中,电压U=()。【单选题】
A.0V
B.4V
C.6V
D.-6V
正确答案:D
答案解析: U=- 2X2-2=-6V
5、变截面杆AC受力如图所示。已知材料弹性模量为E:,杆BC段的截面积为A,杆AB段的截面积为2A,则杆C截面的轴向位移是()。【单选题】
A.
B.
C.
D.
正确答案:A
答案解析:用直接法求轴力,可得:杆C截面的位移是:
6、图示截面对z轴的惯性矩为()。【单选题】
A.
B.
C.
D.
正确答案:A
答案解析: 图示截面对z轴的惯性矩等于圆形截面对z轴的惯性矩减去矩形对z轴的惯性矩。
7、设向量α与向量β的夹角θ =π/3,|α|=1,|β|=2,则|α+β|等于()。【单选题】
A.
B.
C.
D.
正确答案:B
答案解析:本题考查向量代数的基本运算。方法1:方法2:可通过作图来辅助求解。如解图所示:若设β=(2,0),由于α和β的夹角为π/3,则
8、甲、乙为两个互斥的投资方案,甲方案现时点的投资为25万元,此后从第一年年末开始,年运行成本为4万元,寿命期为20年,净残值为8万元;乙方案现时点的投资额为12万元,此后从第一年年末开始,年运行成本为6万元,寿命期也为20年,净残值6万元,若基准收益率为20%,则甲、乙方案费用现值分别为()。 [已知:(p/a,20%,20)=4.8696,(p/f,20%,20)=0. 02608]【单选题】
A.50. 80 万元,-41. 06 万元
B.54. 32 万元,41. 06 万元
C.44.27 万元,41. 06 万元
D.50. 80 万元,44. 27 万元
正确答案:C
答案解析:由于残值可以回收,并没有真正形成费用消耗,故应从费用中将残值减掉。甲方案的费用现值:P=4(P/A,20%,20)+25-8(P/F,20%,20)= 4×4.8696+25-8×0. 02608 = 44.27 万元乙方案的费用现值:P = 6(P/A,20%,20)+ 12-6(P/F,20%,20)=6×4. 8696+12-6×0. 02608=41.06 万元
9、设放大器的输入信号为,放大器的幅频特性如图所示,令,则,则()。【单选题】
A.的出现频率失真
B.的有效值
C.的有效值
D.的有效值
正确答案:C
答案解析:放大器的输入为正弦交流信号,但的频率过高,超出了上限频率放大倍数小于A,因此输出信号的有效值。
10、1mol理想气体(刚性双原子分子),当温度为T时,每个分子的平均平动动能为()。【单选题】
A.3/2RT
B.5/2RT
C.3/2kT
D.5/2kT
正确答案:C
答案解析:分子的平均平动动能公式,分子的平均动能公式,刚性双原子分子自由度i=5,但此题问的是每个分子的平均平动动能而不是平均动能,故正确选项为C。
下面小编为大家准备了 电气工程师 的相关考题,供大家学习参考。
A.-1 B.+127 C.-127 D.+1
提示:根据补码与真值的转换得到。
下列不属于开关柜应具有的防误功能的有()。
A.防止谈分合断路器; B.防止带负荷分离隔离开关;
C.防止接地开关合上时送电; D.防止影响设备安全运行的大量尘埃进入。
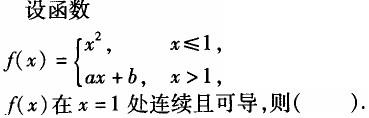
B.a=0,b=1
C.a=2,b=-1
D.a=-1,b=2
 的收敛半径为2,则幂级数
的收敛半径为2,则幂级数 的收敛区间是( )。
的收敛区间是( )。
A. (-2,2) B. (-2,4) C. (0,4) D. (-4,0)

声明:本文内容由互联网用户自发贡献自行上传,本网站不拥有所有权,未作人工编辑处理,也不承担相关法律责任。如果您发现有涉嫌版权的内容,欢迎发送邮件至:contact@51tk.com 进行举报,并提供相关证据,工作人员会在5个工作日内联系你,一经查实,本站将立刻删除涉嫌侵权内容。
- 2020-10-29
- 2021-05-15
- 2020-09-02
- 2020-08-30
- 2021-02-16
- 2020-12-06
- 2021-08-05
- 2021-02-03
- 2021-01-17
- 2020-08-05
- 2021-01-11
- 2021-05-02
- 2021-08-27
- 2020-12-06
- 2021-07-11
- 2021-01-21
- 2021-03-17
- 2020-12-11
- 2021-07-18
- 2020-09-17
- 2021-03-16
- 2020-12-29
- 2020-09-26
- 2021-02-19
- 2021-07-10
- 2021-05-29
- 2021-08-10
- 2021-02-10
- 2021-02-04
- 2020-10-24