网友您好, 请在下方输入框内输入要搜索的题目:
A、b点的需求价格弹性等于c点的需求价格弹性
B、b点的需求价格弹性大于1
C、b点的需求价格弹性小于1
D、b点的需求价格弹性等于1
已知过点(0,4),斜率为-1的直线l与抛物线C:y2—2px(b>;0)交于A,B两点.
(I)求C的顶点到2的距离;
(Ⅱ)若线段AB中点的横坐标为6,求C的焦点坐标.
(3)点M是弧AB的中点,CM交AB于点N,若
AB=4,求MN·MC的值.

A、单线段;间距2mm的双直线段且涂实心;间距为2mm的双直线段(空心)
B、单线段;间距为1mm的双直线段且涂实心;间距为1mm的双直线段(空心)
C、间距为2mm的双直线段且涂实心;单线段;间距为2mm的双直线段(空心)
D、间距为1mm的双直线段且涂实心;单线段;间距为1mm的双直线段(空心)
⑵在复平面内,复数6+5i, -2+3i 对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数是
(A)4+8i
(B)8+2i
(C)2+4i
(D)4+i
问题1:如图,若点C为线段AB的中点,则中点的六种表示是_
(1)若已知AC=3,求BC,则用哪一种表示方法:_
(2)若已知AC=3,求AB,则用哪一种表示方法:_
(3)若已知AB=6,求AC,则用哪一种表示方法:_
问题2:如图,若OC为AOB的平分线,则角平分线的六种表示是_
(1)若已知BOC=35,求AOB,则用哪一种表示方法:_
(2)若已知BOC=35,求AOC,则用哪一种表示方法:_
(3)若已知AOB=70,求BOC,则用哪一种表示方法:_
1.如图,AB=12cm,M为线段AB的中点,点C在线段MB上,且MC:CB=1:2,则线段AC的长度为( )A.6cm B.7cm C.8cm D.9cm
答案:C
解题思路:
试题难度:三颗星
知识点:中点的应用
2.如图所示,AOB=BOC,COD=AOD=3AOB,则COD的度数为( )A.100 B.120 C.135 D.150
答案:B
解题思路:
试题难度:三颗星
知识点:角的计算
3.如图,已知线段BC=7 cm,点C是线段AB的中点,求AB的长解:如图,_即AB的长为14cm;BC=AC;AB=2BC;点C是线段AB的中点;BC=7;AC=7;AB=27=14;AB=AC+BC=14以上空缺处依次所填正确的是( )A. B. C. D.
答案:C
题思路:
试题难度:三颗星
知识点:中点过程训练
4.如图,已知OC平分AOB,AOB=70,求AOC的度数解:如图,OC平分AOB_即AOC的度数为35AOB=2AOC;AOC=COB;AOB=70;AOC=COB=35以上空缺处依次所填正确的是( )A. B. C. D.
答案:B
解题思路:
试题难度:三颗星
知识点:角平分线过程训练
5.已知:如图,线段AB=20 cm,AD=12 cm,点C是线段AD的中点,求BC的长解:如图,点C是线段AD的中点_AB=20BC=AB-AC =20-6 =14即BC的长为14cm;AC=CD;AD=2AC;AB=20;AD=12;AC=12=6;CD=12=6;AC=CD=6以上空缺处依次所填正确的是( )A. B. C. D.
答案:A
解题思路:
试题难度:三颗星
知识点:中点过程训练
6.如图,已知OC平分AOB,OD平分AOC,且COD=25,求BOC的度数解:如图,OD平分AOC_COD=25AOC=225=50OC平分AOB_AOC=50_即BOC的度数为50AOD=COD;AOC=2COD;AOC=BOC;BOC=AOC;BOC=50;BOC=2DOC=225=50以上空缺处依次所填正确的是( )A. B. C. D.
答案:D
解题思路:
试题难度:三颗星
知识点:角平分线过程训练
(1)当MN∥AC且BM=12.5时,求线段MN的长。
(2)当MN与AC不平行时,△CMN可能成为直角三角形吗?若可能,请写出线段CN长的取值范围;若不可能,请说明理由。
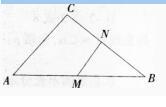

(1)当MN∥AC且BM=12.5时,求线段MN的长。
(2)当MN与AC不平行时,△CMN可能成为直角三角形吗 若可能,请写出线段CN长的取值范围;若不可能,请说明理由。
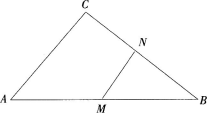

①当CN=15,且点M运动到切点P位置时,△CMN为直角三角形;
②当15<CN<20时,半圆O与直线AB有两个交点,当点M运动到这两个交点的位置时,△CMN为直角三角形:
③当0<CN<15时.半圆O与直线AB相离.即点M在AB边上运动时,均在半圆O外,∠CMN<90°,此时△CMN不可能为直角三角形。
所以当15≤CN<20时.ACMN可能为直角三角形:
【应试指导】设线段的垂直平分线上任一点为P(χ,y),则

即

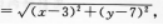
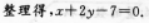
B.(-4,1)
C.(-2,4)
D.(-1,2)
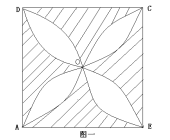 ,四边形ABCD是边长为1的正方形,弧AOB,BOC,COD,DOA均为半圆,则阴影部分的面积为
,四边形ABCD是边长为1的正方形,弧AOB,BOC,COD,DOA均为半圆,则阴影部分的面积为
更多 “几何初步计算及过程训练专项训练一含答案” 相关考题
- 货油舱设置的高位报警装置,在货油被灌装到()的液位时,能发出警报。A、90%B、95%C、98%
- 通脉四逆汤主治:()A、下利清谷,里寒外热,汗出而厥者B、呕而脉弱,小便复利,身有微热,见厥者C、下利腹胀满,身体疼痛者D、手足厥寒,脉细欲厥者E、下利后脉绝,手足厥冷,脉不还者
- 拉伸力的大小是实现()的基本因素之一。
- 威尼斯画派
- 为使拉制能连续进行,就不能在拉制过程中产生断线和拉细现象。因此,拉制条件还必须满足拉伸应力()模具出口处线材的屈服极限的条件。A、大于B、小于C、等于D、不大于
- 不是静电放电的形式是:()A、刷形放电B、火花放电C、球形放电
- 在装卸货、洗舱作业结束后,将货物管线内残留的货物清除的过程称为:()A、扫舱B、扫线C、洗线
- 高导电铝杆与普通铝杆相比,其导电性能更好。
- 火焰阻挡器应安装在()。A、管口B、管中间C、管里
- 结胸证悉具,见下列何证预后不良?()A、烦躁B、短气C、但头汗出D、谵语E、潮热