网友您好, 请在下方输入框内输入要搜索的题目:

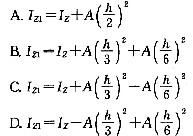

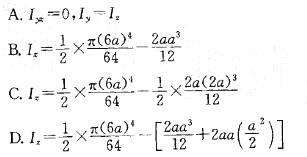
 ,故结论B不正确。
,故结论B不正确。
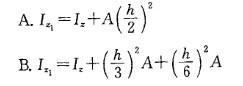
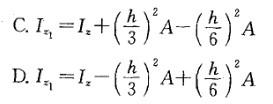



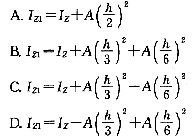


第五章 相交线与平行线周周测3一 选择题1. 如图,已知12,则下列结论一定成立的是() AAB/CD BAD/BC CBD D34 2. 下列图形中,能由1=2得到AB/CD的是() A B C D 3. 如图,能判定 的条件是( ) A B C D 4. 对于图中标记的各角,下列条件能推理得到ab的是( ) A1=2 B2=4 C3=4 D1+4=180 5. 如图,下列条件中: (1)B+BCD=180;(2)1=2;(3)3=4;(4)B=5能判定ABCD的条件个数有() A1个 B2个 C3个 D4个 6. 如图,下列条件中,不能判断直线 的是( ) A13 B23 C45 D241807. 如图,已知1=70,要使ABCD,则须具备另一个条件() A2=70 B2=100 C2=110 D3=1108. 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的定理是() A同位角相等两直线平行 B同旁内角互补,两直线平行 C内错角相等两直线平行 D平行于同一条直线的两直线平行9. 如图,能判定ECAB的条件是() AB=ACE BA+ACD=180 CACE=DCE DA=ACE10. 如图,下列能判定ABCD的条件有() (1)B+BCD=180; (2)1=2; (3)3=4; (4)B=5 A1个 B2个 C3个 D4个 11. 过一点画已知直线的平行线,则( ) A有且只有一条 B有两条 C不存在 D不存在或只有一条 12. 如图,能判断直线ABCD的条件是 () A1=2 B3=4 C1+3=180 o D3+4=180 o 二 填空题13. 如图,两直线ab被第三条直线c所截,若1=50,2=130,则直线ab的位置关系是_ 14. 在同一平面内,_叫作平行线. 15. 如图,直线a、b被直线c所截,若满足 ,则a、b平行(写出一个即可) 16. 已知 为平面内三条不同直线,若 , ,则 与 的位置关系是 .三 解答题 17. 看图填空: 如图,1的同位角是 , 1的内错角是 , 如果1=BCD,那么 ,根据是 ; 如果ACD=EGF,那么 ,根据是 .18. 如图,已知1=2,AC平分DAB,试说明DCAB. 19. 已知:如图,A=F,C=D求证:BDCE 20. 如图,已知:B=D+E,试说明:ABCD 第五章 相交线与平行线周周测3 参考答案与解析一、选择题1.B 2.D 3.D 4.D 5.C 6.B 7.C 8.C 9.D 10. C 11.D 12.D 二、填空题13.平行 14.不相交的两条直线 15.1=2(答案不唯一) 16.平行 三、解答题 17.EFG BCD,AED DEBC 内错角相等,两直线平行 CDGF 同位角相等,两直线平行 18. 解:AC平分DAB,1=CAB.1=2,CAB=2,DCAB.19. 证明:A=F,ACDF,C=CEF.C=D,D=CEF,BDCE.20.解:过点E向右作EM/CD,则D=DEM.B=D+E, 第 5 页 共 5 页
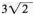
解析:矩形内的点到相对顶点的距离平方和相等,即PA2+PC2=PB2+PD2,即32+52=42+PD2,
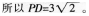
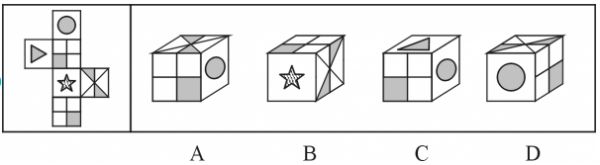
B. 如图所示
C. 如图所示
D. 如图所示





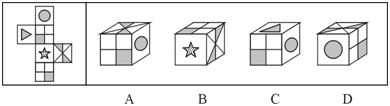
B. 如图所示
C. 如图所示
D. 如图所示

解析:



B.如上图所示
C.如图示
D.如图
更多 “七年级数学下册第五章相交线与平行线周周测3(5.2)含答案解析” 相关考题
- ( 难度:中等)关于参数传递说法正确的()A.A:基本数据类型参数传递的是值,引用数据类型参数传递的是引用B.B:不管是基本数据类型还是引用数据类型都是值传递C.C:基本数据类型参数传递的是数据值,引用数据类型参数传递的是对象D.D:基本数据类型参数是值传递,引用数据类型传递是引用传递
- 期望理论可以用( )来加以表述。A。结果=效价×期望 B。动机=效价×工具 C.动机=效价×期望×工具 D.结果=效价×期望×工具
- 在众多激励理论中,不考虑人的内在心态,而是注重行为及其结果的理论是( )。 A。目标设置理论 B.强化理论 C.能力与机遇理论 D.认知评价理论
- 国防是一个庞大的系统工程,国防强固必须优化各相关要素,包括( )、( )、( )、( )、( )、( )、( )、( )。A.政治清明,经济实力雄厚B.武装力量强大C.全民爱国,关心国防D.实行进攻性的军事战略E.国防科技工业先进配套F.国防工程设施完善G.建立广泛的国际联盟H.国防动员体制机制先进有效
- Response对象的()方法可以将缓冲区中的页面内容立即输出到客户端。A. WriteB. EndC. ClearD. Flush
- “单选(5分)“我能,无限可能”和“to be NO.1”体现的是哪种需要( )A. 自我实现的需要B. 归属和爱的需要C. 生理需要D. 安全需要
- 当贷款的本金或利息逾期 90 天时,应单独核算。
- 商业银行吸收企事业单位或人人的存款是现金存款。
- 信息化战争涉及的内容包括:A. 信息是核心资源B. 信息化军队C. 信息化、智能化武器装备D. 多维信息化战场E. 信息化战争性质
- 本行为付款行,对方行为收款行的网内往来汇划业务是发出贷方报单业务。