网友您好， 请在下方输入框内输入要搜索的题目：
请你写出一个有一根为1的一元二次方程：____________．
19世纪60年代，麦克斯韦列出了表达电磁基本定律的()
A 、一元方程式
B 、一元二次方程组
C 、四元方程组
D 、二元二次方程组
如果2是一元二次方程x2＋bx＋2＝0的一个根，那么常数b的值为________________．
-3
一元二次方程x2+x-2=0 的两根之积是（ ）
A．-1
B．-2
C．1
D．2
B.x2-10x+64=0
C.x2-20x+8=0
D.x2-20x+64=0
灌云县四队中学九年级月测试卷数 学 （总分：150分 时间：100分钟） 制卷人：曹如全一、选择题（每小题4分，共32分）1一元二次方程3=5x的二次项系数和一次项系数分别是（ ） A3，5 B3，5 C3，0 D5，0下列方程中，是关于x的一元二次方程的是（ ） A B 2=0 C D 3. 关于的一元二次方程的一个根为1，则实数=（ ）A B或 C D4方程的解的情况是（ ）A有两个不相等的实数根 B没有实数根C有两个相等的实数根 D有一个实数根 5若关于x的一元二次方程的两个根为，则这个方程是（）A. B. C. D.6根据下列表格对应值：3.243.253.260.020.010.03判断关于的方程的一个解的范围是（ ）A.3.24 B.3.243.25C.3.253.26 D.3.263.287.以3、4为两边长的三角形的第三边长是方程的根，则这个三角形的周长为（ ）A.15或12 B.12 C.15 D.以上都不对8某种花卉每盆的盈利与每盆的株数有一定的关系，每盆植3株时，平均每株盈利4元；若每盆增加1株，平均每株盈利减少0.5元，要使每盆的盈利达到15元，每盆应多植多少株？设每盆多植x株，则可以列出的方程是（）A. B. C. D.二填空题（每小题4分，共32分）9. 方程的二次项系数是 ，一次项系数是 ，常数项是 .10关于x的一元二次方程中，则一次项系数是 . 11一元二次方程的根是 .12若关于的一元二次方程化成一般形式后二次项的系数为1，一次项的系数为1，则m的值为。13若，那么代数式的值是。14某地2005年外贸收入为2.5亿元，2007年外贸收入达到了4亿元，若平均每年的增长率为，则可以列出方程为 .15请你写出一个有一根为1，另一个根介于和1之间的的一元二次方程： 16如果是方程的两个根，那么；。班 级 姓 名 考 号 灌云县四队中学九年级月测试卷答题纸数 学 （总分：150分 时间：100分钟） 制卷人：曹如全一、选择题（每小题4分，共32分）题号12345678答案二、填空题（每小题4分，共32分）9_ _ _ 10._11._ 12._13._ 14._15._ 16. _ _ 三、解答题（共86分）17选择适当方法解下列方程：（每小题6分，共36分）(1) (2) （3） （4） （） （）18（本题8分）当为何值时，关于的一元二次方程有两个相等的实数根？此时这两个实数根是多少？19（本题10分）已知x1是一元二次方程的一个解， 且，求的值.20（本题8分）某种电脑病毒传播非常快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染请你用学过的知识分析，每轮感染中平均一台电脑会感染几台电脑？若病毒得不到有效控制，3轮感染后，被感染的电脑会不会超过700台？21（本题10分）某超市经销一种成本为40元/kg的水产品，市场调查发现，按50元/kg销售，一个月能售出500kg，销售单位每涨1元，月销售量就减少10kg，针对这种水产品的销售情况，超市在月成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应定为多少？22（本题14分）将一块长18米，宽15米的矩形荒地修建成一个花园（阴影部分）所占的面积为原来荒地面积的三分之二（精确到0.1m）（1）设计方案1（如图1）花园中修两条互相垂直且宽度相等的小路（2）设计方案2（如图2）花园中每个角的扇形都相同以上两种方案是否都能符合条件?若能，请计算出图中的小路的宽和图中扇形的半径；若不能符合条件，请说明理由（） 图1 图2灌云县四队中学九年级月测试卷答案数 学 一、选择题（每小题4分，共32分）题号12345678答案BACABBBA二、填空题（每小题4分，共32分）9_3_ _3_ _0_ 10._- 1_ 11. 12. _- 1_ 13._ _- 6_ 14. 15.（答案不唯一）如：16. _2_ _- 1_ 三、解答题（共86分）17选择适当方法解下列方程：（每小题6分，共36分）(1) (2) （3） （4） （） （） 18（本题8分）当为何值时，关于的一元二次方程有两个相等的实数根？此时这两个实数根是多少？ M= （3分） （5分）19（本题8分）已知x1是一元二次方程的一个解， 且，求的值. a+b=40（3分） = 20（5分）20（本题10分）某种电脑病毒传播非常快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染请你用学过的知识分析，每轮感染中平均一台电脑会感染几台电脑？若病毒得不到有效控制，3轮感染后，被感染的电脑会不会超过700台？解：设每轮感染中平均每一台电脑会感染x台电脑，依题意得：1+x+（1+x）x=81， 整理得，（2分） 则x+1=9或x+1=-9， 解得（舍去）（3分）， +x）=729700（3分） 答：每轮感染中平均每一台电脑会感染8台电脑，3轮感染后，被感染的电脑会超过700台（2分）21（本题10分）某超市经销一种成本为40元/kg的水产品，市场调查发现，按50元/kg销售，一个月能售出500kg，销售单位每涨1元，月销售量就减少10kg，针对这种水产品的销售情况，超市在月成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应定为多少？解：销售单价定为每千克x元时，月销售量为：500(x50)10千克而每千克的销售利润是:(x40)元，(x40)500(x50)10=8000，（2分） 即：140x+4800=0， 解得：（4分） 当销售单价定为每千克60元时，月销售量为：500(6050)10=400(千克)，月销售单价成本为： 40400=16000(元)； 由于1600010000，而月销售成本不能超过10000元，所以销售单价无法定为每千克60元（2分）当销售单价定为每千克80元时，月销售量为：500(8050)10=200(千克)，月销售单价成本为： 40200=8000(元)；由于800010000，而月销售成本不能超过10000元，所以销售单价应定为每千克80元（2分）22（本题14分）将一块长18米，宽15米的矩形荒地修建成一个花园（阴影部分）所占的面积为原来荒地面积的三分之二（精确到0.1m）（1）设计方案1（如图1）花园中修两条互相垂直且宽度相等的小路（2）设计方案2（如图2）花园中每个角的扇形都相同以上两种方案是否都能符合条件?若能，请计算出图中的小路的宽和图中扇形的半径；若不能符合条件，请说明理由 图1 图2解都能.（1）设小路宽为x，则18x+16xx21815，即x234x+1800，（3分）解这个方程，得xhttp:/，（3分）即x6.6. （1分）答：小路宽为6.6米（1分）（2）设扇形半径为r，则3.14r21815，（2分）即r257.32，（2分）所以r7.6. （1分）答：扇形半径为7.6米. （1分）以上答案仅供参考，如果错误，敬请谅解！
一、考题回顾
【教学过程】
(一)引入新课
复习回顾一元二次方程的一般形式以及求根公式。
提出问题：一元二次方程的根与方程中的系数之间有怎样的关系呢?
引出课题。
(四)小结作业
提问：今天有什么收获?引导学生回顾：一元二次方程根与系数的关系以及推导证明过程。
作业：课后练习。
【板书设计】
【答辩题目解析】
1.教学目标是什么?
【参考答案】
(1)知识与技能
学生知道一元二次方程根与系数的关系，并会应用根与系数关系解决问题。
(2)过程与方法
学生能够借助问题的引导，发现、归纳并证明一元二次方程根与系数的关系，在探究过程中，感受由特殊到一般地认识事物的规律。
(3)情感态度价值观
通过探索一元二次方程的根与系数的关系，激发发现规律的积极性，鼓励勇于探索的精神。
一、考题回顾
二、考题解析
【教学过程】
(一)引入新课
复习旧知：回顾之前学习过哪些方程，并对一元一次方程的定义进行回顾。
总结：明确本节课学习初中阶段的最后一种方程，《一元二次方程》。
【板书设计】
【答辩题目解析】
1.谈一谈你本节课导入的设计意图是什么?
2.一元二次方程、二次函数、一元二次不等式之间的联系是什么?
这样的设计既可以考察学生对之前知识的掌握情况，还能够为今天学习一元二次方程的概念打下基础。
2、三者之间联系非常的紧密：一元二次方程的根为二次函数与x轴交点的横坐标;一元二次不等式的解集其中大于0的部分为二次函数在x轴上方函数图象的定义域，小于0部分为二次函数在x轴下方函数图象的定义域。
【教师甲】
设置问题：请同学们根据下列问题，只列出含未知数的方程：
预设：学生会分别列出两个方程。
教师要求学生分别整理成方程左侧降幂排序，右侧为零的形式，然后引导学生完成下面两件事：对比“一元一次方程”的定义，为这类方程定义一个名称——一元二次方程。再请学生自行写出几个不同的一元二次方程，并提炼出一元二次方程的一般表达式。
【教师乙】
上课开始。提问：什么是“一元一次方程”？请你根据“一元一次方程”的定义，给出“一元二次方程”的定义，并举出几个“一元二次方程”的例子。在学生举例的基础上，提炼出“一元二次方程”的一般表达式。
请完成下列任务：
（1）请分析两位老师引入“一元二次方程”概念设计方案的各自的特点。（15分）
（2）在教学中，当引入一个新的数学概念之后，往往通过例题、习题加深对概念的理解。请针对“一元二次方程”概念，设计不同难度的两道例题和两道练习题，加深学生对“一元二次方程”概念的理解。（15分）
（1）教学活动是师生积极参与、交往互动、共同发展的过程。有效的教学活动是学生学与教师教的统一，学生是学习的主体，教师是学习的组织者、引导者和合作者。数学教学活动应激发学生的学习兴趣，调动学生积极性，引发学生思考，鼓励学生的创造性思维。在教学的过程中教师应培养学生良好的数学学习习惯，使学生掌握恰当的数学学习方法。也注重以学生的认知发展水平和已有经验为基础，面向全体学生，采取启发式和因材施教的教学。学生在生动活泼的、主动的教学课堂中，更容易吸收知识，但也应注重多种学习方式相结合，除接受学习外，动手实践、主动探索与合作交流同样是学习数学的重要方式。
教师甲的教学方案，相对于乙教师来说，更加非常符合素质教育的要求。
（2）针对“一元二次方程”概念，设计不同难度的两道例题和两道练习题，题目的难度应适当，目的是加深学生对“一元二次方程”概念的理解。
①进一步了解一元二次方程的概念；
②进一步了解-元二次方程的多种解法（配方法、公因式法、因式分解法等)；
③会运用判别式判断一元二次方程根的情况；
④通过相关问题的讨论，在理解相关知识的同时，休会数学思想方法，积累数学活动经验。 问题：
根据上述教学目标，完成下列任务：
(1)为了落实上述教学目标①、②，请设计一个教学片段，并说明设计意图；
(2)配方法是解一元二次方程的通性解法，请设计问题串，以帮助学生进一步理解配方法在解一元二次方程中的作用。
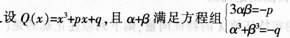(1)证明α+β是Q（χ）=0的根；(3分)
(2)写出以α3和β3为根的一元二次方程。(4分)
更多 “初三数学试题：灌云县四队中学2014年九年级10月月考数学试题及答案” 相关考题
- 1926年，国民政府出师北伐。北伐的主要对象不包括（）A、吴佩孚B、张勋C、张作霖D、孙传芳
- “毫不利己，专门为人”是毛泽东同志在1939年12月发表的（）一文中向全党发出的号召。A、《为人民服务》B、《整顿党的作风》C、《纪念白求恩》D、《改造我们的学习》
- 单选题发生洪水、城市内涝时，在积水中行走应穿（）。A 长筒雨靴B 凉鞋C 运动鞋D 拖鞋
- 汽车垂直网站发文模块的标准动作是：确保每日更新、每篇文章有效期不超过一周、根据不同主题，制定对应的标题和内容（）
- 高速巡航时发动机直驱模式，为本田独有模式
- 在与客户洽谈初期的沟通内容正确的是（）。A、介绍车辆性能B、推荐促销车型C、谈与车无关的话题D、告知促销活动
- 什么是精神文明建设“三下乡”活动？
- 简述循环系统和血细胞的功能。
- 放电试验在蓄电池充电完毕，静置（）分钟后进行.A、30B、15C、45D、60
- ECON绿色节能辅助系统对节省油耗有显著的作用，这是因为它能将发动机动力输出和（）切换到节油模式？A、空调功率B、车辆灯光C、车辆胎压