网友您好, 请在下方输入框内输入要搜索的题目:
在平面直角坐标系中,点A(m,6)与点B(2.5,n)关于原点对称,则A、B两点之间的距离为( )。
A.5
B.12
C.13
D.8.5
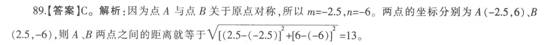
已知A,B是抛物线y2=4x上的两个动点,且|AB|=3,则当AB的中点M到y轴的距离最短时,点M的横坐标是____.
下列平面图形中,即是轴对称图形又是中心对称图形的是( )

A.A
B.B
C.C
D.D
 , 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是
, 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是B.关于原点对称
C.关于直线y=x轴对称
D.以上均错

2015-2016九年级数学期中考试试题一、 选择题(共30分)1、已知点A (a, 3)与点B(1, b)关于原点对称,则a+b的值为 ()A、 -4B、-2C、2D、42、下列图形中,是中心对称图形的是() TOC o 1-5 h z 3、抛物线y=x2-mx-m2+1的图像过原点,则m的值为 ()A1B1 C -1D 04、一元二次方程x2+2x+2=0根的情况是()A 无实数根 B只有一个实数根C有两个相等的实数根D 有两个不相等的实数根5、抛物线y=-2x2不具有的性质是()A、开口向下B、对称轴是y轴 C、当x0时,y随x的增大而减小D、y有最小值6、如图,已知。0是4ABD的外接圆,AB是。0的直径,CD是炫,/ABD=58A、58?B、32?C、38?30? TOC o 1-5 h z 7、若一个三角形的两边长分别为 3和6,第三边长满足方程x2-6x+8=0,则此三 角形的周长为()A、11B、11 或 13 C、10D、138、如图,四边形ABCD内接于。0,已知/ ADC=140?,则/ AOC的度数为()A、80?B、100?C、60?D、40?9、某生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠 送一件,全组共互赠了 180件,如果全组有x名学生,则根据题意列出的方程是(A、x(x+1)=182 B、x(x-1)=182 C、x(x-1)=182X2D、x(x+1)=182X2 TOC o 1-5 h z 10、二次函数y=ax2+bx+c的图像如图所示,贝 abc, b2-4ac, 2a+b, a+b+c这四 个式子中,值为正数的有()A、 4个B、3个 C、2个D、1个二、填空题(共12分)11、如图,A、B、C是。0上的三点,/BAC=30?, WJ/BOC的大小是()。12、关于x的一元二次方程(a-2) x2+x+a2-4=0的一个根为0,则方程的另一个 根为()。13、如图,将RtABC绕直角顶点C顺时针旋转90 ,得到AA B C,连接 AA,若/ 1=26 ,则/ B的大小是()14、在函数y=x2+2x+2中,若-5&x&5,那么函数y的最大值是(三、解答题(共11题,78分) 15、(5 分)解方程:(2x-3) 2=x2 16、(5分)已知关于x的一元二次方程 mx2+x+1=0.(1)当该方程有一个根为1时,确定m的值;(2)当该方程有两个不相等的实数根时,确定 m的取值范围17、(5 分)如图,AB 是。0 的直径,/CAB= / DAB。求B证 AC=AD.18、(5分)已知关于x的二次函数的图像的顶点坐标为(-1,2),且图像过点(1,-3)。(1)求该二次函数的关系式;(2)写出它的开口方向、对称轴。19、(7分)如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点, DAE旋转后能与 DCF重合.(1)旋转中心是哪一点?(2)旋转的最小角度为多少?(3)如果连接EF,判断4DEF的形状,并说明理由20、(7)分如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度; ABC的顶点均在格点上。(1)画出 ABC关于坐标原点0成中心对称的 A1B1C1(2)以O为旋转中心将 ABC逆时针旋转90得4A2B2c2,画出AzB2c2并直 接写出C2的坐标。21 (7分)如图,AB是。0的实景,CD是。0的一条炫,且 CDLAB于点E证明:(1)/BCO=/D;若CD= 4J2 , AE=2 ,求。O的半径.22、(7分)已知抛物线y=-2x2+4x

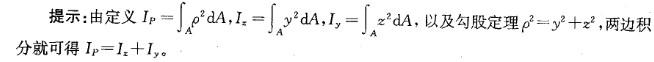
B.12
C.13
D.8.5
(2.5,-6),则 4、B 两点之间的距离就等于
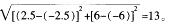
B.12
C.13
D.8.5
(2.5,-6),则 4、B 两点之间的距离就等于
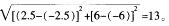
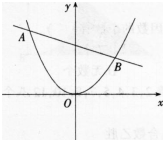
(1)直线ι经过一个定点C,试求出点C的坐标;(2分)
(2)若m=-1,已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合),且△ABP的面积为(3√13)/2,求点P的坐标。(6分)


 , 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是
, 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是B.关于原点对称
C.关于直线y=x轴对称
D.以上均错

更多 “陕西安康旬阳桐木初级中学2016届九年级上学期期中考试数学试题” 相关考题
- 志贺菌感染中,哪一项不正确()A、传染源是患者和带菌者,无动物宿主B、宋内志贺菌多引起轻型感染C、福氏志贺菌感染易转变为慢性D、急性中毒性菌痢以小儿多见E、感染后免疫期长且巩固
- 安装接线图是表示电气设备、元件的连接关系,用于配线、查线、接线等,一般可分为()。A、单元接线图B、单线接线图C、互连接线图D、端子接线图E、中断法接线图
- 下列选项中说法正确的是()A、应多吃冷饮B、应多喝含咖啡因的饮料C、不宜将饮料代替白开水D、应多吃些高热量的巧克力
- 所谓“三股势力”,就是宗教极端势力、民族分裂势力和国际恐怖势力。()
- 单选题Using the CMYK color model, the color purple is produced by combining cyan and which other color?()A GreenB MagentaC YellowD Black
- 在电气图中,前向通路上的信息流方向应按()的方向布置。
- 大楼水箱液位控制器连接导线最少为二根,即可控制水泵启动,停止。
- 单选题The proper safety guidelines for handling any device specific consumables can be found in which of the following documentation?()A Material Safety Data SheetsB Installation GuidesC Consumer ReportsD Devices Parts Catalog
- 钾缺乏可以引起甲状腺功能异常。
- 单选题Which of the following is a reason black toner is used in color printers?()A It decreases the print speed in color laser printers.B It prevents moir patterns when printing color photographs.C It reduces the cost per page when printing gray scale documents.D It makes the color toner resistant to smudging when wet.
- 2013年武汉市七一中学九年级3月月考语文试题-
- 备考2019年电大《现代汉语专题1》试题资料附答案【备考资料_
- 电大2019年《行政组织学》多套资料题汇编附答案【备考篇】_
- 电大2019年行政法与行政诉讼法选择题及考核测验题五份汇编附答案【备考资料_
- 呕心沥血整理2019年二级建造师考试建设工程施工管理个人学习笔记及试题汇编附答案精编备考可编辑_
- 2019年自考当代中国政治制度试题资料汇编附全答案【电大备考】_
- 2019年自学考试当代中国政治制度复习备考资料汇编附答案汇编【备考资料_
- 2019年自学考试当代中国政治制度自考复习资料试题汇编附答案【考前资料】_
- 2019年最新国家开 放大学电大《 城市管理学 》网络核心课形考网考作业及答案_
- 2019年最新国家开 放大学电大《管理英语3》网络核心课形考网考作业附全答案备考_