网友您好, 请在下方输入框内输入要搜索的题目:
A.先求b后求a
B. 先确定a后求b
C. a,b可以同时求得
D. 先求x,再求a和b
利用历史资料分析法的各种具体应用方法建立成本模型时,计算步骤正确的有()
A、先求b后求a
B、先确定a后求b
C、a,b可以同时求得
D、先求r,再求a和b
E、先求x和y,再求a和b
用布尔代数化简法求图2—1所示的事故树的最小割集。
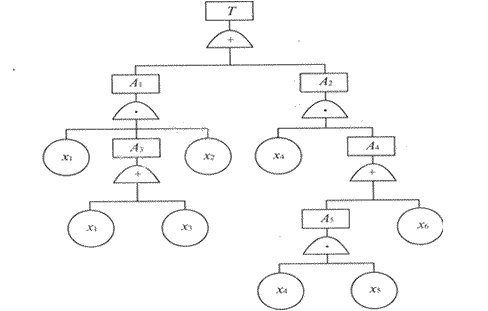
用布尔代数化简法求事故树最小割集的步骤为( )。

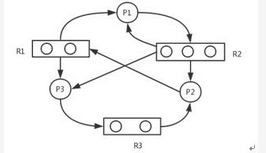
B.可以化简的,其化简顺序为P3→P1→P2
C.可以化简的,其化简顺序为P2→P1→P3
D.不可以化简的,因为P1、P2、P3申请的资源都不能得到满足
因为P3非阻塞且非孤立,所以可以化简。将其所用资源归还资源图后,P1获得R2,即可运行,然后也可以化简,最后P2可以运行。
黑龙江省哈尔滨市三年(2020-2022)中考数学真题分类汇编-03解答题一分式的化简求值(共3小题)1(2022哈尔滨)先化简,再求代数式()的值,其中x2cos45+12(2021哈尔滨)先化简,再求代数式()的值,其中a2sin4513(2020哈尔滨)先化简,再求代数式(1)的值,其中x4cos301二一元一次不等式的应用(共3小题)4(2022哈尔滨)绍云中学计划为绘画小组购买某种品牌的A、B两种型号的颜料,若购买1盒A种型号的颜料和2盒B种型号的颜料需用56元;若购买2盒A种型号的颜料和1盒B种型号的颜料需用64元(1)求每盒A种型号的颜料和每盒B种型号的颜料各多少元;(2)绍云中学决定购买以上两种型号的颜料共200盒,总费用不超过3920元,那么该中学最多可以购买多少盒A种型号的颜料?5(2021哈尔滨)君辉中学计划为书法小组购买某种品牌的A、B两种型号的毛笔若购买3支A种型号的毛笔和1支B种型号的毛笔需用22元;若购买2支A种型号的毛笔和3支B种型号的毛笔需用24元(1)求每支A种型号的毛笔和每支B种型号的毛笔各多少元;(2)君辉中学决定购买以上两种型号的毛笔共80支,总费用不超过420元,那么该中学最多可以购买多少支A种型号的毛笔?6(2020哈尔滨)昌云中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需用136元;若购买2个大地球仪和1个小地球仪需用132元(1)求每个大地球仪和每个小地球仪各多少元;(2)昌云中学决定购买以上两种地球仪共30个,总费用不超过960元,那么昌云中学最多可以购买多少个大地球仪?三一次函数综合题(共1小题)7(2020哈尔滨)已知:在平面直角坐标系中,点O为坐标原点,直线AB与x轴的正半轴交于点A,与y轴的负半轴交于点B,OAOB,过点A作x轴的垂线与过点O的直线相交于点C,直线OC的解析式为yx,过点C作CMy轴,垂足为M,OM9(1)如图1,求直线AB的解析式;(2)如图2,点N在线段MC上,连接ON,点P在线段ON上,过点P作PDx轴,垂足为D,交OC于点E,若NCOM,求的值;(3)如图3,在(2)的条件下,点F为线段AB上一点,连接OF,过点F作OF的垂线交线段AC于点Q,连接BQ,过点F作x轴的平行线交BQ于点G,连接PF交x轴于点H,连接EH,若DHEDPH,GQFGAF,求点P的坐标四二次函数综合题(共2小题)8(2022哈尔滨)在平面直角坐标系中,点O为坐标原点,抛物线yax2+b经过点A(,),点B(,),与y轴交于点C(1)求a,b的值;(2)如图1,点D在该抛物线上,点D的横坐标为2过点D向y轴作垂线,垂足为点E点P为y轴负半轴上的一个动点,连接DP,设点P的纵坐标为t,DEP的面积为S,求S关于t的函数解析式(不要求写出自变量t的取值范围);(3)如图2,在(2)的条件下,连接OA,点F在OA上,过点F向y轴作垂线,垂足为点H,连接DF交y轴于点G,点G为DF的中点,过点A作y轴的平行线与过点P所作的x轴的平行线相交于点N,连接CN,PB,延长PB交AN于点M,点R在PM上,连接RN,若3CP5GE,PMN+PDE2CNR,求直线RN的解析式9(2021哈尔滨)在平面直角坐标系中,点O为坐标系的原点,抛物线yax2+bx经过A(10,0),B(,6)两点,直线y2x4与x轴交于点C,与y轴交于点D,点P为直线y2x4上的一个动点,连接PA(1)求抛物线的解析式;(2)如图1,当点P在第一象限时,设点P的横坐标为t,APC的面积为S,求S关于t的函数解析式(不要求写出自变量t的取值范围);(3)如图2,在(2)的条件下,点E在y轴的正半轴上,且OEOD,连接CE,当直线BP交x轴正半轴于点L,交y轴于点V时,过点P作PGCE交x轴于点G,过点G作y轴的平行线交线段VL于点F,连接CF,过点G作GQCF交线段VL于点Q,CFG的平分线交x轴于点M,过点M作MHCF交FG于点H,过点H作HRCF于点R,若FR+MHGQ,求点P的坐标五全等三角形的判定与性质(共1小题)10(2020哈尔滨)已知:在ABC中,ABAC,点D、点E在边BC上,BDCE,连接AD、AE(1)如图1,求证:ADAE;(2)如图2,当DAEC45时,过点B作BFAC交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图2中的四个等腰三角形,使写出的每个等腰三角形的顶角都等于45六矩形的性质(共1小题)11(2022哈尔滨)已知矩形ABCD的对角线AC,BD相交于点O,点E是边AD上一点,连接BE,CE,OE,且BECE(1)如图1,求证:BEOCEO;(2)如图2,设BE与AC相交于点F,CE与BD相交于点H,过点D作AC的平行线交BE的延长线于点G,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形(AEF除外),使写出的每个三角形的面积都与AEF的面积相等七正方形的性质(共1小题)12(2021哈尔滨)已知四边形ABCD是正方形,点E在边DA的延长线上,连接CE交AB于点G,过点B作BMCE,垂足为点M,BM的延长线交AD于点F,交CD的延长线于点H(1)如图1,求证:CEBH;(2)如图2,若AEAB,连接CF,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形(AEG除外),使写出的每个三角形都与AEG全等八圆的综合题(共3小题)13(2022哈尔滨)已知CH是O的直径,点A、点B是O上的两个点,连接OA,OB,点D,点E分别是半径OA,OB的中点,连接CD,CE,BH,且AOC2CHB(1)如图1,求证:ODCOEC;(2)如图2,延长CE交BH于点F,若CDOA,求证:FCFH;(3)如图3,在(2)的条件下,点G是一点,连接AG,BG,HG,OF,若AG:BG5:3,HG2,求OF的长14(2021哈尔滨)已知O是ABC的外接圆,AB为O的直径,点N为AC的中点,连接ON并延长交O于点E,连接BE,BE交AC于点D(1)如图1,求证:CDE+BAC135;(2)如图2,过点D作DGBE,DG交AB于点F,交O于点G,连接OG,OD,若DGBD,求证:OGAC;(3)如图3,在(2)的条件下,连接AG,若DN,求AG的长15(2020哈尔滨)已知:O是ABC的外接圆,AD为O的直径,ADBC,垂足为E,连接BO,延长BO交AC于点F(1)如图1,求证:BFC3CAD;(2)如图2,过点D作DGBF交O于点G,点H为DG的中点,连接OH,求证:BEOH;(3)如图3,在(2)的条件下,连接CG,若DGDE,AOF的面积为,求线段CG的长九作图应用与设计作图(共1小题)16(2020哈尔滨)如图,方格纸中每个小正方形的边长均为1,线段AB和线段CD的端点均在小正方形的顶点上(1)在图中画出以AB为边的正方形ABEF,点E和点F均在小正方形的顶点上;(2)在图中画出以CD为边的等腰三角形CDG,点G在小正方形的顶点上,且CDG的周长为10+连接EG,请直接写出线段EG的长一十作图-轴对称变换(共1小题)17(2022哈尔滨)如图,方格纸中每个小正方形的边长均为1,ABC的顶点和线段EF的端点均在小正方形的顶点上(1)在方格纸中画出ADC,使ADC与ABC关于直线AC对称(点D在小正方形的顶点上);(2)在方格纸中画出以线段EF为一边的平行四边形EFGH(点G,点H均在小正方形的顶点上),且平行四边形EFGH的面积为4,连接DH,请直接写出线段DH的长一十一作图-平移变换(共1小题)18(2021哈尔滨)如图,方格纸中每个小正方形的边长均为1个单位长度,ABC的顶点和线段DE的端点均在小正方形的顶点上(1)在方格纸中将ABC向上平移1个单位长度,再向右平移2个单位长度后得到MNP(点A的对应点是点M,点B的对应点是点N,点C的对应点是点P),请画出MNP;(2)在方格纸中画出以DE为斜边的等腰直角三角形DEF(点F在小正方形的顶点上)连接FP,请直接写出线段FP的长一十二条形统计图(共3小题)19(2022哈尔滨)民海中学开展以“我最喜欢的健身活动”为主题的调查活动,围绕“在跑步类、球类、武术类、操舞类四类健身活动中,你最喜欢哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢操舞类的学生人数占所调查人数的25%请你根据图中提供的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)若民海中学共有1600名学生,请你估计该中学最喜欢球类的学生共有多少名20(2021哈尔滨)春宁中学开展以“我最喜欢的冰雪运动项目”为主题的调查活动,围绕“在冰球、冰壶、短道速滑、高山滑雪四种冰雪运动项目中,你最喜欢哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢短道速滑的学生人数占所调查人数的40%请你根据图中提供的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)若春宁中学共有1500名学生,请你估计该中学最喜欢高山滑雪的学生共有多少名21(2020哈尔滨)为了丰富同学们的课余生活,冬威中学开展以“我最喜欢的课外活动小组”为主题的调查活动,围绕“在绘画、剪纸、舞蹈、书法四类活动小组中,你最喜欢哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢绘画小组的学生人数占所调查人数的30%请你根据图中提供的信息回答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)若冬威中学共有800名学生,请你估计该中学最喜欢剪纸小组的学生有多少名参考答案与试题解析一分式的化简求值(共3小题)1(2022哈尔滨)先化简,再求代数式()的值,其中x2cos45+1【解答】解:(),当x2cos45+12+1+1时,原式2(2021哈尔滨)先化简,再求代数式()的值,其中a2sin451【解答】解:原式,当a2sin451211时,原式3(2020哈尔滨)先化简,再求代数式(1)的值,其中x4cos301【解答】解:原式,x4cos3014121,原式二一元一次不等式的应用(共3小题)4(2022哈尔滨)绍云中学计划为绘画小组购买某种品牌的A、B两种型号的颜料,若购买1盒A种型号的颜料和2盒B种型号的颜料需用56元;若购买2盒A种型号的颜料和1盒B种型号的颜料需用64元(1)求每盒A种型号的颜料和每盒B种型号的颜料各多少元;
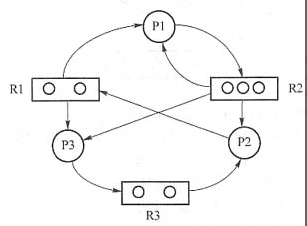
B.可以化简的,其化简顺序为P3->P1->P2
C.可以化简的,其化简顺序为P2->P1->P3
D.不可以化简的,因为P1、P2、P3申请的资源都不能得到满足
B:合并
C:夸大
D:位移
E:压盖
逻辑函数化简的方法主要有()化简法和()化简法。
正确答案:公式;卡诺图
逻辑函数化简的方法主要有()化简法和()化简法。
正确答案:公式;卡诺图
分析混联电路可采用逐次等效化简方法化简。
正确答案:正确
更多 “黑龙江省哈尔滨市三年(20202022)中考数学真题分类汇编03解答题” 相关考题
- ( 难度:中等)以下哪种不是Hive支持的数据类型A.longB.xmlC.IntD.string
- 2016年7月12日,由南海某声索国单边发起的仲裁案结果出笼,大大增加了南海的复杂化形势,这个国家是()
- 以下说法正确的是( )。A.心理正常包含了心理健康与心理不健康B.频繁体验到抑郁情绪即患有抑郁症C.有偏执型人格倾向说明是这个人患有人格障碍D.某同学因求职失败而情绪低落感到无助,可以判断他患上了抑郁症
- 形位公差带形状是距离为公差值t的两平行平面内区域的有______。A.平面度B.任意方向的线的直线度C.给定一个方向的线的倾斜度D.任意方向的线的位置度E.面对面的平行度
- 固定资产、无形资产、长期待摊费用等物权形式存在的资产不属于金融资产。
- 租赁是资产的所有权与使用权相分离的交易.
- 公平理论认为,员工会将自己的产出与投入比与别人的产出与投入比进行比较.这里的“产出”是指( )。 A.工作经验 B。工作报酬 C.工作绩效 D.工作承诺
- 银行发生现金长款时,经查找确实无法归还,经批准坐银行收益处理,通过其他业务收入核算。
- 全体人民共同富裕,应该由全体人民___________?
- ( )是精神分析学派的开创者。A.荣格B.弗洛伊德C.阿德勒D.埃里克森
- 2016南通航运职业技术学院单招语文模拟试题及答案-
- 2016南通航运职业技术学院单招数学模拟试题及答案-
- 施工员岗位实务知识测试题(全考点)模拟卷及参考答案(96)-
- 施工员岗位实务知识测试题(全考点)模拟卷及参考答案(56)-
- 施工员岗位实务知识测试题(全考点)模拟卷及参考答案(65)-
- 施工员岗位实务知识测试题(全考点)模拟卷及参考答案(7)-
- 施工员岗位实务知识测试题(全考点)模拟卷及参考答案(72)-
- 施工员岗位实务知识测试题(全考点)模拟卷及参考答案(66)-
- 施工员岗位实务知识测试题(全考点)模拟卷及参考答案(83)-
- 施工员岗位实务知识测试题(全考点)模拟卷及参考答案(第13套)-