网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设acosx+bsinx是R到R的函数,V={acosx+bsinx |a,b∈R }是函数集合,对?∈V,令D??(x)=?′(x),即D将一个函数变成它的导函数,证明D是V到V上既单又满的映射。
参考答案
参考解析
解析:
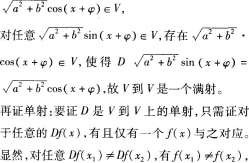
因此D是V到V上的单射。
综上可知V到V既是单射又是满射,即D是V到V上既单又满的映射。

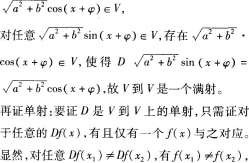
因此D是V到V上的单射。
综上可知V到V既是单射又是满射,即D是V到V上既单又满的映射。
更多 “设acosx+bsinx是R到R的函数,V={acosx+bsinx |a,b∈R }是函数集合,对?∈V,令D??(x)=?′(x),即D将一个函数变成它的导函数,证明D是V到V上既单又满的映射。” 相关考题
考题
设R、N分别表示实数、整数和自然数集,下面定义函数f1、f2、f3:f1:R→R,f(x)=2xf2:N→N×N,f(n)=f
设R、N分别表示实数、整数和自然数集,下面定义函数f1、f2、f3: f1:R→R,f(x)=2x f2:N→N×N,f(n)=<n,n+1> f3:N→N,f(x)=x mod 3,x除以3的余数 则下面说法正确的是( )。A.f1和f2是单射但不是满射函数B.f1和f3都是满射函数C.f2是双射函数D.以上说法全都是错误的
考题
设R(U)是属性集U上的关系模式。X,Y是U的子集。若对于R(U)的任意一个可能的关系R,R中不可能存在两个元组在X上的属性值相等,而在Y上的属性值不等,则称( )。A.Y对X完全函数依赖B.R属于2NFC.X为U的候选码D.Y函数依赖于X
考题
设R,N分别表示实数、整数和自然数集,下面定义函数f1,f2,f3: fl:R→R,f(x)=2x f2:N→N×N,f(n)=<n,n+1> f3:N→N,f(x)=x mod 3,x除以3的余数 则下面说法正确的是A.n和f2是单射但不是满射函数B.f1和f3都是满射函数C.f2是双射函数D.以上说法全都是错误的
考题
已知函数fun的原型是“void fun(int *x, int ”,变量v1、v2的定义是“int v1, v2; ”,则下列选项中,对函数fun调用正确的是( )。
A. fun(v1,B.fun(v1,v2);C.fun(D.fun(
考题
设关系模式R(A,B,C,D,E,F),函数依赖集F={A_C,C_A,B—AC,D一,AC,BD—A}。1)求出R的候选码及F的最小函数依赖集。2)将R分解为3NF,使其既具有无损连接性又具有函数依赖保持性。
考题
设R(U)是在属性U上的关系模式,X,Y是U的子集,若对于R(U)的任意一个可能的关系r,r中的任意两个元组在X上的属性值相等,那么在Y上的属性值也相等,则称( )。A.r函数依赖于XB.r对X完全函数依赖C.X为U的侯选码D.R属于2NF
考题
下面表示纯虚函数的成员函数是( )。A.virtual int v(int);B.void v(int) =0;C.virtual void v() =0;D.virtual void v(int) { }
考题
单选题函数f(u,v)由关系式f[xg(y),y]=x+g(y)确定,其中函数g(y)可微,且g(y)≠0,则∂2f/∂u∂v=( )。A
g′(v)/g(v)B
-g′(v)/g2(v)C
g′(v)/g2(v)D
-g′(v)/g(v)
考题
单选题设f(x)是R上的函数,则下列叙述正确的是()。A
f(x)f(-x)是奇函数B
f(x)|f(x)|是奇函数C
f(x)-f(-x)是偶函数D
f(x)+f(-x)是偶函数
热门标签
最新试卷