网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设u=u(x),v=v(x)是可微的函数,则有d(uv)=()
A.udu+vdv
B.u'dv+v'du
C.C.udv+vdu
D.udv-vdu
B.u'dv+v'du
C.C.udv+vdu
D.udv-vdu
参考答案
参考解析
解析: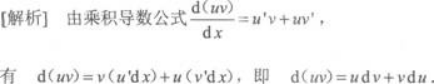
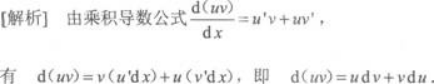
更多 “设u=u(x),v=v(x)是可微的函数,则有d(uv)=()A.udu+vdv B.u'dv+v'du C.C.udv+vdu D.udv-vdu” 相关考题
考题
设随机变量X,y独立同分布,且X~N(0,σ^2),再设U=aX+by,V=aX-bY,其中a,b为不相等的常数.求:
(1)E(U),E(V),D(U),D(V),;
(2)设U,V不相关,求常数A,B之间的关系.
考题
设随机变量X,Y独立同分布,且P(X=i)=,i=1,2,3.
设随机变量U=max{X,Y},V=min{X,Y}.
(1)求二维随机变量(U,V)的联合分布;(2)求Z=UV的分布;
(3)判断U,V是否相互独立?(4)求P(U=V).
考题
(Ⅰ)设函数u(x),ν(x)可导,利用导数定义证明[u(x)ν(x)]’=u’(x)ν(x)+u(x)ν’(x);
(Ⅱ)设函数u1(x),u2(x),…,un(x)可导,f(x)=u1(x)u2(x)…un(x),写出f(x)的求导公式.
考题
在F[x]中,任一对多项式f(x)与g(x)都有最大公因式,且存在u(x),v(x)∈F(x),满足哪个等式?()A、u(x)f(x)v(x)g(x)=d(x)B、u(x)f(x)+v(x)g(x)=d(x)C、u(x)f(x)/v(x)g(x)=d(x)D、u(x)/f(x)+v(x)/g(x)=d(x)
考题
单选题设f(u,v)是二元可微函数,z=f(y/x,x/y),则x∂z/∂x-y∂z/∂y=( )。A
-yf1′/x+xf2′/yB
2(-yf1′/x+xf2′/y)C
-yf1′/x+2xf2′/yD
-yf1′/x+f2′/y
考题
填空题设向量u(→)=3i(→)-4j(→),v(→)=4i(→)+3j(→),且二元可微函数f(x,y)在点P处有∂f/∂u(→)|P=-6,∂f/∂v(→)|P=17,则df|P=____。
考题
单选题设f(u,v)是二元可微函数,z=f(y/x,x/y),则x∂z/∂x-y∂z/∂y=( )。A
-yf1′/x-xf2′/yB
-yf1′/x+xf2′/yC
2(-yf1′/x+xf2′/y)D
2(-yf1′/x-xf2′/y)
考题
单选题函数f(u,v)由关系式f[xg(y),y]=x+g(y)确定,其中函数g(y)可微,且g(y)≠0,则∂2f/∂u∂v=( )。A
g′(v)/g(v)B
-g′(v)/g2(v)C
g′(v)/g2(v)D
-g′(v)/g(v)
考题
单选题若函数u=xy·f[(x+y)/xy],f(t)为可微函数,且满足x2∂u/∂x-y2∂u/∂y=G(x,y)u,则G(x,y)必等于( )。A
x+yB
x-yC
x2-y2D
(x+y)2
考题
单选题设u=sinx+φ(sinx+cosy)(φ为可微函数),且当x=0时,u=sin2y,则∂u/∂y=( )。A
sinxsiny+cosysinyB
sinxsiny+cosycosyC
2(sinxsiny+cosysiny)D
2(sinxsiny+cosycosy)
考题
单选题设f(u,v)是二元可微函数,z=f(y/x,x/y),则x∂z/∂x-y∂z/∂y=( )。A
2(yf1′/x+xf2′/y)B
2(yf1′/x-xf2′/y)C
2(-yf1′/x+xf2′/y)D
2(-yf1′/x-xf2′/y)
考题
单选题设向量u(→)=3i(→)-4j(→),v(→)=4i(→)+3j(→),且二元可微函数f(x,y)在点P处有∂f/∂u(→)|P=-6,∂f/∂v(→)|P=17,则df|P=( )。A
10dx+5dyB
10dx+15dyC
15dx+10dyD
5dx+10dy
考题
单选题函数f(u,v)由关系式f[xg(y),y]=x+g(y)确定,其中函数g(y)可微,且g(y)≠0,则∂2f/∂u∂v=( )。A
g′(v)/g2(v)B
-g′(v)/g2(v)C
g(v)/g2(v)D
-g(v)/g2(v)
热门标签
最新试卷