网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
均质圆盘重W,半径为R,绳子绕过圆盘,两端各挂重Q和P的物块,绳与盘之间无相对滑动,且不计绳重,则圆盘的角加速度为( )。
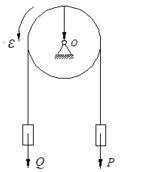

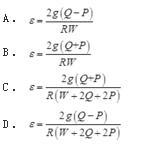
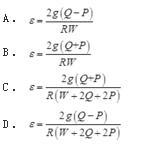
参考答案
参考解析
解析: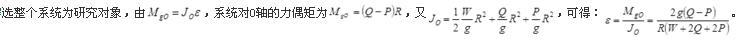
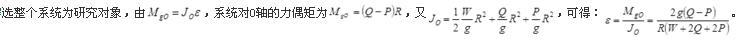
更多 “均质圆盘重W,半径为R,绳子绕过圆盘,两端各挂重Q和P的物块,绳与盘之间无相对滑动,且不计绳重,则圆盘的角加速度为( )。 ” 相关考题
考题
一绳索跨过匀质滑轮B,绳的一端挂一重物A;另一端缠绕一匀质圆柱C,如图所示。已知重物A的质量为mA;定滑轮B和圆柱C的质量分别为mB和mC,它们的半径均为r。绳的质量略去不计,它对定滑轮无相对滑动。设mB=mC=2mA,则定滑轮与圆柱之间绳索的拉力T为( )。
考题
杆OA绕固定轴O转动,圆盘绕动轴A转动,已知杆长l=20cm,圆盘r=10cm,在图示位置时,杆的角速度及角加速度分别为w=4rad/s,ε=3rad/s2;圆盘相对于OA的角速度和角加速度分别为wr=6rad/s,εr=4rad/s2。则圆盘上M1点绝对加速度为( )。
A.a1=363cm/s2
B.a1=463cm/s2
C.a1=563cm/s2
D.a1=663cm/s2
考题
质量为m,半径为R的均质圆盘,绕垂直于图面的水平轴O转动,其角速度为ω,在图示瞬时,角加速度为零,盘心C在其最低位置,此时将圆盘的惯性力系向O点简化, 其惯性力主矢和惯性力主矩的大小分别为:
考题
确定物体绕某个轴的转动惯量,可以由理论计算也可通过实验测定。
(1)用积分计算质量为m,半径为R的均质薄圆盘绕其中心轴的转动惯量。
(2)该圆盘质量未知,可用如图9所示的实验方法测得该圆盘绕中心轴的转动惯量。在圆盘的边缘绕有质量不计的细绳,绳的下端挂一质量为m的重物,圆盘与转轴间的摩擦忽略不计。测得重物下落的加速度为a,求圆盘绕其中心轴的转动惯量。
考题
如右图,一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动,当小圆盘围绕大圆盘中心转过90°后,小圆盘运动过程中扫过的面积是多少平方厘米?(π取3)( )
A. 18 B. 15
C. 12 D. 10
考题
质量为m,半径为R的均质圆盘,绕垂直于图面的水平轴O转动,其角速度为ω,在图4-78示瞬时,角加速度为零,盘心C在其最低位置,此时将圆盘的惯性力系向O点简化,其惯性力主矢和惯性力主矩的大小分别为()。
考题
长度为L的轻绳固定在水平天花板A点和竖直墙B点,绳上挂一定滑轮(质量不计),滑轮下吊一重物C,两绳之间夹角为θ,当绳子缓慢从B点移到动B’点后,则以下说法正确的是()A、绳的拉力不变B、绳的拉力变小C、θ角变大D、θ角减小
考题
一转动惯量为J的圆盘绕一固定轴转动,起初角速度为W0。设它所受阻力矩与转动角速度成正比,即M=-KW(k为正的常数),则圆盘的角速度为W0/2时其角加速度a=(),圆盘的角速度从W0变为W0/2时所需的时间为()。
考题
从一个质量均匀分布的半径为R的圆盘中挖出一个半径为R/2的小圆盘,两圆盘中心的距离恰好也为R/2。如以两圆盘中心的连线为x轴,以大圆盘中心为坐标原点,则该圆盘质心位置的x坐标应为()A、R/4B、R/6C、R/8D、R/12
考题
半径为R具有光滑轴的定滑轮边缘绕一细绳,绳的下端挂一质量为m的物体绳的质量可以忽略,绳与定滑轮之间无相对滑动若物体下落的加速度为a,则定滑轮对轴的转动惯量J=()。
热门标签
最新试卷