网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
在如下线性约束条件下：2x+3y<=30；x+2y>=10；x>=y；x>=5；y>=0，目标函数2x+3y的极小值为（ ）。

A.16.5
B.17.5
C.20
D.25

参考答案

参考解析
解析：根据题意，画出可行区域，如图虚线阴影部分。

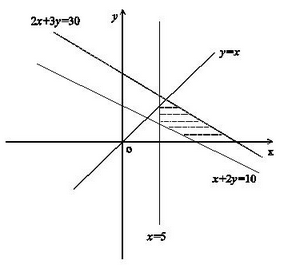
显然，x=5与x+2y=10相交处时有最小值，联立得x=5，y=2.5，因此2x+3y最小值为25+32.5=17.5。
更多 “在如下线性约束条件下：2x+3y=10；x>=y；x>=5；y>=0，目标函数2x+3y的极小值为（ ）。A.16.5 B.17.5 C.20 D.25” 相关考题
考题 以下结论正确的是()。 A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
查看答案
考题 （ 9 ）有如下的函数定义：int Xfun(int x){int y=x;{int x=10; y+=x;}return x+y;}通过表达式 Xfun(5) 调用该函数，则得到的返回值为 【 9 】 。
查看答案
考题 试题(53)、(54)线性规划问题就是求出一组变量，在一组线性约束条件下，使某个线性目标函数达到极大（小）值。满足线性约束条件的变量区域称为可行解区。由于可行解区的边界均是线性的（平直的），属于单纯形，所以线性目标函数的极值只要存在，就一定会在可行解区边界的某个顶点达到。因此，在求解线性规划问题时，如果容易求出可行解区的所有顶点，那么只要在这些顶点处比较目标函数的值就可以了。例如，线性规划问题：max S=x+y（求S=x+y的最大值）；2x+y≤7，x+2y≤8，x≥0，y≥0的可行解区是由四条直线2x+y=7，x+2y;8，x=0，y=0围成的，共有四个顶点。除了原点外，其他三个顶点是(53)。因此，该线性规划问题的解为 (54) 。(53)A. (2,,(0,7),(3.5,0)B. (2,3),(0,4),(8,0)C. (2,3),(0,7),(8,O)D. (2,3),(0,4),(3.5,0)(54)A. x=2, y=3B.x=0, y=7C.x=0, y=4D.x=8, y=0
查看答案
考题 函数z=f（x，y）处可微分，且fx'（x0，y0）=0，fy'（x0，：y0）=0，则f （x，y）在P0（x0，y0）处有什么极值情况？ A.必有极大值 B.必有极小值 C.可能取得极值 D.必无极值
查看答案
考题 已知函数f(x,y)在点(0,0)的某个邻域内连续，且 ，则A.点(0,0)不是f(x,y)的极值 B.点(0,0)是f(x,y)的极大值点 C.点(0,0)是f(x,y)的极小值点 D.根据所给条件无法判断点(0,0)是否为f(x,y)的极值点
查看答案
考题 函数z=f(x,y)在P0 (x0,y0)处可微分，且f'x (x0,y0)=0，f'y(x0,y0)=0，则f(x,y)在P0 (x0,y0)处有什么极值情况？ A.必有极大值 B.必有极小值 C.可能取得极值 D.必无极值
查看答案
考题 函数y = f (x)在点x = x0,处取得极小值，则必有：
查看答案
考题 求函数(x，y)=x2+y2在条件2x+3y=1下的极值．
查看答案
考题 随机变量X与Y相互独立，X的均值为5，标准差也为5，Y的均值为9，方差为16，则V=2X+3Y的均值与方差分别为（ ）。A. 22； 164 B. 22； 244 C. 37； 164 D. 37； 244
查看答案
考题 2X+3Y=60 5X-2Y=14 3X-5Y=42（） A.3 B.4 C.5 D.6
查看答案
考题 若集合M={（x，y）｜ 3x一2y=-1），N={（x，y）｜ 2x+3y=8}，则M∩N=（）A.（1，2） B.{1，2} C.{（1，2）} D.φ
查看答案
考题 如，点A,B,O,的坐标分别为（4,0）,（0,3）,（0,0）,若（x,y）是三角形AOB中的点，则2x+3y的最大值为（ ）A.6 B.7 C.8 D.9 E.12
查看答案
考题 在如下线性约束条件下：2x+3y=10；x>=y；x>=5；y>=0，目标函数2x+3y的极小值为（　）A. 16.5 B.17.5 C. 20 D.25
查看答案
考题 设函数f（x，y）＝x3+y3-3xy，则（）。A、f（0，0）为极大值B、f（0，0）为极小值C、f（1，1）为极大值D、f（1，1）为极小值
查看答案
考题 对于两个独立的随机变量X，Y服从正态分布，即X~N（4，9），Y~N（1，4）则，E（2X+3Y）=（）。A、9B、11C、13D、7
查看答案
考题 设y=f（x）是微分方程y"-2y’+4y=0的一个解，又f（x0）O，f’（x0）=0，则函数f（x）在点x0（）．A、取得极大值B、取得极小值C、的某个邻域内单调增加D、的某个邻域内单调减少
查看答案
考题 直线2x+3y=4，在y轴上的截距是（）A、4/3B、－4/3C、2D、－2
查看答案
考题 单选题随机变量X的平均值为5，标准差也为5，随机变量Y的均值为9，方差为l6，则V=2X+3Y的均值与方差为(　　)。A 37，164B 37，244C 22，164D 22，244
查看答案
考题 单选题随机变量X与Y相互独立，X的均值为5，标准差也为5，Y的均值为9，方差为16，则V＝2X+3Y的均值与方差分别为（　　）。A 22；164B 22；244C 37；164D 37；244
查看答案
考题 单选题设确定了函数y＝g（x），则（　　）。A x＝0是函数y＝g（x）的驻点，且是极大值点B x＝0是函数y＝g（x）的驻点，且是极小值点C x＝0不是函数y＝g（x）的驻点D 存在x＝0的一个小邻域，y＝g（x）是单调的
查看答案
考题 单选题直线2x+3y=4，在y轴上的截距是（）A 4/3B －4/3C 2D －2
查看答案
考题 单选题已知方程x2y2＋y＝1（y＞0）确定y为x的函数，则（　　）。A y（x）有极小值，但无极大值B y（x）有极大值，但无极小值C y（x）既有极大值又有极小值D 无极值
查看答案
考题 单选题函数z=f（x，y）在P0（x0，y0）处可微分，且f′（x0，y0）=0，fy′（x0，y0）=0，则f（x，y）在P0（x0，y0）处有什么极值情况？（）A 必有极大值B 必有极小值C 可能取得极值D 必无极值
查看答案
考题 单选题设x⊕y＝2x＋3y，x⊙y＝xy，且x、y均为正整数，若当x⊙y＝6时，x⊕y取得最小值，则x等于（　　）。A 2B 6C 4D 3
查看答案
考题 单选题y＝f（x）是方程y″－2y′＋4y＝0的一个解，若f（x0）＞0，f′（x0）＝0，则函数f（x）（　　）。A 在x0点取得极大值B 在x0的某邻域单调增加C 在x0点取得极小值D 在x0的某邻域单调减少
查看答案
考题 单选题设函数z＝f（x，y）的全微分为dz＝xdx＋ydy，则点（0，0）（　　）。A 不是f（x，y）的连续点B 不是f（x，y）的极值点C 是f（x，y）的极大值点D 是f（x，y）的极小值点
查看答案
考题 单选题可微函数f（x，y）在点（x0，y0）取得极小值，下列结论正确的是（　　）。A f（x0，y）在y＝y0处的导数等于零B f（x0，y）在y＝y0处的导数大于零C f（x0，y）在y＝y0处的导数小于零D f（x0，y）在y＝y0处的导数不存在
查看答案
热门标签
最新试卷