网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设a3+3ax2+8为增函数。
A. x0 D.x0
A. x0 D.x0
参考答案
参考解析
解析: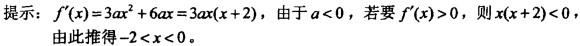
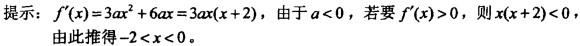
更多 “设a3+3ax2+8为增函数。 A. x0 D.x0” 相关考题
考题
凯恩斯货币需求理论认为()。
A.交易性货币需求是收入的增函数B.交易性货币需求是收入的减函数C.投机性货币需求是利率的减函数D.投机性货币需求是利率的增函数E.预防性货币需求是利率的增函数
考题
设R(t)表示可靠度函数,F(t)表示累积故障分布函数,则以下描述正确的是( )。A.R(t)是[0,∞)区间内的非减函数,且0≤R(t)≤1B.R(t)是[0,∞]区间内的非增函数,且0≤R(t)≤lC.在(0,∞)区间内,R(t)+F(t)=lD.F(t)在[0,∞]区间内的非减函数,且0≤F(t)≤1E.F(t)在[0,∞]区间内的非增函数
考题
设f(x)为连续函数,F(x)是f(x)的原函数,则( )。(A) 当f(x)是奇函数时,F(x)必为偶函数(B) 当f(x)是偶函数时,F(x)必为奇函数(C) 当f(x)是周期函数时,F(x)必为周期函数(D) 当f(x)是单增函数时,F(x)必为单增函数(E) 当f(x)是单减函数时,F(x)必为单减函数
考题
请教:2008 年春季中国精算师资格考试-01数学基础(一)第1大题第1小题如何解答?
【题目描述】
1.设f(x)为连续函数,F(x)是f(x)的原函数,则( )。
(A) 当f(x)是奇函数时,F(x)必为偶函数
(B) 当f(x)是偶函数时,F(x)必为奇函数
(C) 当f(x)是周期函数时,F(x)必为周期函数
(D) 当f(x)是单增函数时,F(x)必为单增函数
(E) 当f(x)是单减函数时,F(x)必为单减函数
考题
设f(x)是连续函数,F(x)是f(x)的原函数,则()。
A.当f(x)是奇函数时,F(x)必是偶函数
B.当f(x)是偶函数时,F(x)必是奇函数
C.当f(x)是周期函数时,F(x)必是周期函数
D.当f(x)是单调增函数时,F(x)必是单调增函数
考题
单选题如果奇函数f(x)在区间[a,b](0<a<b)上是增函数,且最小值为2,那么f(x)在区间[-b,-a]上是( ).A
增函数且最小值为-2B
增函数且最大值为-2C
减函数且最小值为-2D
减函数且最大值为-2
考题
单选题设a0,则当满足条件()时,函数f(x)=ax3+3ax2+8为增函数。A
x-2B
-2C
x0D
x-2或x0
热门标签
最新试卷