网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设直角三角形的三边为a、b、c,内切圆直径为2r,外接圆直径为2R,若a、b、c成等差数列,
求证:
(I)内切圆的半径等于公差;
(Ⅱ)2r、a、b、2R也成等差数列.
求证:
(I)内切圆的半径等于公差;
(Ⅱ)2r、a、b、2R也成等差数列.
参考答案
参考解析
解析:(I)由题意知,2R=c,∵a+b=r+r+χ+y,(如图a=χ+r,b=y+r)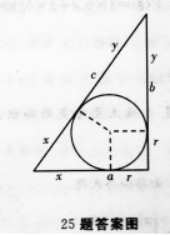
又∵c=χ+y→2r=a+b-c.
设公差为d,则三边为b-d,b,b+d,则有(b-d)2+b2=(b+d)2
得6=4d,即三边a、b、c分别等于3d、4d、5d,
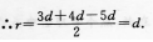
(Ⅱ)由(I)可知2r、a、b、2R分别为2d、3d、4d、5d,∴其也为等差数列.

又∵c=χ+y→2r=a+b-c.
设公差为d,则三边为b-d,b,b+d,则有(b-d)2+b2=(b+d)2
得6=4d,即三边a、b、c分别等于3d、4d、5d,
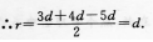
(Ⅱ)由(I)可知2r、a、b、2R分别为2d、3d、4d、5d,∴其也为等差数列.
更多 “设直角三角形的三边为a、b、c,内切圆直径为2r,外接圆直径为2R,若a、b、c成等差数列, 求证: (I)内切圆的半径等于公差; (Ⅱ)2r、a、b、2R也成等差数列.” 相关考题
考题
(2R,3S)-(-)-2-羟基-3-氯丁二酸的对映体的构型和旋光性为:()。
A、(2R,3S)-(-)B、(2R,3S)-(+)C、(2S,3R)-(-)D、(2S,3R)-(+)
考题
设车轮作无滑动的滚动,角速度ω,角加速度ε,0点的加速度a0及半径R均为已知,由此可求得A点的加速度aA在Y轴上的投影为( )A、aAy=2RεB、aAy=-RC、aAy=-2RD、aAy=-2Rε
考题
以CDMA的码片为时间和距离的单位,假设施主基站最大覆盖半径为R,直放站的最大覆盖半径为r,基站与直放站之间的距离为D。直放站的前反向总的群延时为t。接入信道的搜索窗口宽度为()A、MAX[R,r+D+t]B、MAX[2R,2r+D+t]C、MAX[2R,2r+2D+t]D、MAX[2R,2r+2D+2t]
考题
单选题弯曲试验时,如直径或多边形横截面()的产品,其试样横截面为产品横截面。A
外接圆直径不大于40mmB
内切圆直径不大于40mmC
外接圆直径不大于50mmD
内切圆直径不大于50mm
考题
单选题(2R,3S)-(-)-2-羟基-3-氯丁二酸的对映体的构型和旋光性为()。A
(2R,3S)-(-)B
(2R,3S)-(+)C
(2S,3R)-(-)D
(2S,3R)-(+)
考题
单选题设车轮作无滑动的滚动,角速度ω,角加速度ε,0点的加速度a0及半径R均为已知,由此可求得A点的加速度aA在Y轴上的投影为( )A
aAy=2RεB
aAy=-RC
aAy=-2RD
aAy=-2Rε
考题
单选题以CDMA的码片为时间和距离的单位,假设施主基站最大覆盖半径为R,直放站的最大覆盖半径为r,基站与直放站之间的距离为D。直放站的前反向总的群延时为t。接入信道的搜索窗口宽度为()A
MAX[R,r+D+t]B
MAX[2R,2r+D+t]C
MAX[2R,2r+2D+t]D
MAX[2R,2r+2D+2t]
考题
单选题螺旋桨的()直径称螺旋桨的直径,螺距一般由叶根部向外逐渐增加,H0.7R或H2R/3的含义是()。A
叶根圆/压力面2R/3或0.7R处螺距B
分度圆/吸力面2R/3或0.7R处螺距C
叶梢圆/吸压力面2R/3或0.7R处螺距D
叶梢圆/压力面2R/3或0.7R处螺距
考题
单选题假设某客户风险承受能力评估为2R,他不能购买以下()产品。A
产品风险定级为2R的汇添利B
产品风险定级为3R的基金C
产品风险定级为3R的券商集合理财D
产品风险定级为3R的得利宝
热门标签
最新试卷