网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
已知二次型f(x1,x2,3x)=x^TAx在正交变换x=Qy下的标准形为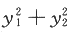 ,且Q的第3列为
,且Q的第3列为 .
.
(Ⅰ)求矩阵A;
(Ⅱ)证明A+E为正定矩阵,其中E为三阶单位矩阵.
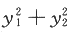 ,且Q的第3列为
,且Q的第3列为 .
.
(Ⅰ)求矩阵A;
(Ⅱ)证明A+E为正定矩阵,其中E为三阶单位矩阵.
参考答案
参考解析
解析:

更多 “已知二次型f(x1,x2,3x)=x^TAx在正交变换x=Qy下的标准形为,且Q的第3列为. (Ⅰ)求矩阵A; (Ⅱ)证明A+E为正定矩阵,其中E为三阶单位矩阵.” 相关考题
考题
已知x1(t)和x2(t)的傅里叶变换分别为X1(f)和X2(f),则卷积x1(t)*x2(t)的傅里叶变换为()。
A、X1(f)X2(f)B、X1(f)*X2(f)C、X1(-f)X2(-f)D、X1(-f)*X2(-f)
考题
设总体X~N(μ,σ2),X1,X2,X3,X4是正态总体X的一个样本,为样本均值,S2为样本方差,若μ为未知参数且σ为已知参数,下列随机变量中属于统计量的有( )。A.X1-X2+X3B.2X3-μC.D.E.
考题
设X~N(μ,σ2),均值μ已知,而方差σ2未知,X1,X2,X3为总体X的样本,下列各式是统计量的有( )。A.X1+3X2+σ2B.X1+2μC.max(X1,X2,X3)D.(X2-μ)2/σE.
考题
二次型f=2x21+3x22+3x23+4x2x3可以由正交变换化作标准型,下列中正确的标准型是( )。
A.2y21+y22-5y23
B.2y21+y22+5y23
C.y21+y22+5y23
D.2y21+y22+4y23
考题
已知二次函数f(x)的二次项系数为实数a,且其图像与直线2x+y=0交点横坐标为1和3.
(1)若方程f(x)+6a=0有两个相等的实数根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数n的取值范围.
考题
设f(x)处处连续,且在x=x1处有f'(x1)=0,在x=x2处不可导,那么( )。
A.x=x1及x=x2都必不是f(x)的极值点
B.只有x=x1是f(x)的极值点
C.x=x1及x=x2都有可能是f(x)的极值点
D.只有x=x2是f(x)的极值点
考题
已知函数
(1)求f(x)单调区间与值域;
(2)设a≥1,函数g(x)=x3-3a2x-2a,x∈[0,1]。若对于任意x1∈[0,1],总存在x0∈[0,1]使g(x0)=f(x1)成立,求a的取值范围。
考题
已知消费者的收入为I,全部用来购买X1,X2,且MU1/P1>MU2/P2,若要达到消费者均衡,需要()A、增加的X1购买,减少X2的购买B、增加X2的购买,减少X1的购买C、X1,X2都增加D、X1,X2都减少。
考题
设f(x)处处连续,且在x=x1处有f'(x1)=0,在x=x2处不可导,那么()。A、x=x1及x=x2都必不是f(x)的极值点B、只有x=x1是f(x)的极值点C、x=x1及x=x2都有可能是f(x)的极值点D、只有x=x2是f(x)的极值点
考题
单选题设f(x)处处连续,且在x=x1处有f'(x1)=0,在x=x2处不可导,那么()。A
x=x1及x=x2都必不是f(x)的极值点B
只有x=x1是f(x)的极值点C
x=x1及x=x2都有可能是f(x)的极值点D
只有x=x2是f(x)的极值点
考题
问答题设f(x)在[a,b]上连续,在(a,b)内可微,若a≥0,证明在(a,b)内存在三个数x1、x2、x3,使f′(x1)=(b+a)f′(x2)/(2x2)=(b2+ab+a2)f′(x3)/(3x32)。
考题
单选题若函数f(x)在区间(a,b)内可导,x1和x2是区间(a,b)内任意两点(x1<x2),则至少存在一点ξ,使( )A
f(b)-f(a)=f′(ξ)(b-a)(a<ξ<b)B
f(b)-f(x1)=f′(ξ)(b-x1)(x1<ξ<b)C
f(x2)-f(x1)=f′(ξ)(x2-x1)(x1<ξ<x2)D
f(x2)-f(a)=f′(ξ)(x2-a)(a<ξ<x2)
考题
单选题已知被测量Y与输入量X1、X2、X3、X4、X5、的估计值分别为y、x1、x2、x3、x4、x5,它们之间的函数关系为y=x1+x2+x3+x4+x5,若输入量X1、X2、X3、X4、X5服从半宽度相同的均匀分布,且相互独立,则被测量Y在相应变化区间内接近( )分布。A
正态B
均匀C
三角D
反正弦
考题
单选题设f(x)在(-∞,+∞)内可导,且对任意x2>x1,都有f(x2)>f(x1),则正确的结论是( )。A
对任意x,f′(x)>0B
对任意x,f′(x)≤0C
函数-f(-x)单调增加D
函数f(-x)单调增加
考题
单选题二次型f(x1,x2,x3)=λx21+(λ-1)λ22+(λ2+1)x23,当满足()时,是正定二次型。()A
λ0B
λ-1C
λ1D
以上选项均不成立
热门标签
最新试卷