网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
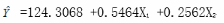
请根据上述结果,从下列备选答案中选出正确答案。
根据计算上述回归方程式的多重判定系数为0.9235,其正确的含义是()。
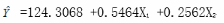
请根据上述结果,从下列备选答案中选出正确答案。
根据计算上述回归方程式的多重判定系数为0.9235,其正确的含义是()。
A.在Y的总变差中,有92.35%可以由解释变量Xl和X2解释
B.在Y的总变差中,有92.35%可以由解释变量Xl解释
C.在Y的总变差中,有92.35%可以由解释变量X2解释
D.在Y的变化中,有92.35%是由解释变量Xl和X2决定的
B.在Y的总变差中,有92.35%可以由解释变量Xl解释
C.在Y的总变差中,有92.35%可以由解释变量X2解释
D.在Y的变化中,有92.35%是由解释变量Xl和X2决定的
参考答案
参考解析
解析:多重判定系数是多元线性回归平方和占总平方和的比例,计算公式为:
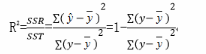
判定系数R2度量了多元线性回归方程的拟合程度,它可以解释为:在因变量Y的总变差中被估计的多元线性回归方程所揭示的比例。
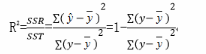
判定系数R2度量了多元线性回归方程的拟合程度,它可以解释为:在因变量Y的总变差中被估计的多元线性回归方程所揭示的比例。
更多 “为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示: 请根据上述结果,从下列备选答案中选出正确答案。 根据计算上述回归方程式的多重判定系数为0.9235,其正确的含义是()。 A.在Y的总变差中,有92.35%可以由解释变量Xl和X2解释 B.在Y的总变差中,有92.35%可以由解释变量Xl解释 C.在Y的总变差中,有92.35%可以由解释变量X2解释 D.在Y的变化中,有92.35%是由解释变量Xl和X2决定的” 相关考题
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下
请根据上述结果,从下列备选答案中选出正确答案。
回归系数β2=0.2562的经济意义为()。A.我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
B.在可支配收人不变的情况下,我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
C.在可支配收入不变的情况下,我国居民家庭居住面积每减少1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
D.我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均减少0.2562千瓦小时
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
请根据上述结果,从下列备选答案中选出正确答案。
根据计算上述回归方程式的多重判定系数为0.9235,其正确的含义是()。A.在Y的总变差中,有92.35%可以由解释变量X1和X2解释
B.在Y的总变差中,有92.35%可以由解释变量X1解释
C.在Y的总变差中,有92.35%可以由解释变量X2解释
D.在Y的变化中,有92.35%是由解释变量X1和X2决定的
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
请根据上述结果,从下列备选答案中选出正确答案。
对于多元线性回归模型,以下假设中正确的有()。A.因变量与自变量之间的关系为线性关系
B.随机误差项的均值为1
C.随机误差项之间是不独立的
D.随机误差项的方差是常数
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
请根据上述结果,从下列备选答案中选出正确答案。
回归系数β2=0.2562的经济意义为()。A.我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
B.在可支配收人不变的情况下,我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
C.在可支配收入不变的情况下,我国居民家庭居住面积每减少1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
D.我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均减少0.2562千瓦小时
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下
请根据上述结果,从下列备选答案中选出正确答案。
根据样本观测值和估计值计算回归系数β2的t统计量,其值为t=8.925,根据显著性水平(a=0.05)与自由度,由t分布表查得t分布的右侧临界值为2.431,因此,可以得出的结论有()。
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
请根据上述结果,从下列备选答案中选出正确答案。
根据样本观测值和估计值计算回归系数β2的t统计量,其值为t=8.925,根据显著性水平(a=0.05)与自由度,由t分布表查得t分布的右侧临界值为2.431,因此,可以得出的结论有()。
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下
请根据上述结果,从下列备选答案中选出正确答案。
根据计算上述回归方程式的多重判定系数为0.9235,其正确的含义是()。A.在Y的总变差中,有92.35%可以由解释变量X1和X2解释
B.在Y的总变差中,有92.35%可以由解释变量置解释
C.在Y的总变差中,有92.35%可以由解释变量X2解释
D.在Y的变化中,有92.35%是由解释变量X1和X2决定的
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
请根据上述结果,从下列备选答案中选出正确答案。
检验回归方程是否显著,正确的假设是()。
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下
请根据上述结果,从下列备选答案中选出正确答案。
检验回归方程是否显著,正确的假设是()。A.H0:β1=β2=0;H1:β1≠β2≠0
B.H0:β1=β2≠0;H1:β1≠β2=0
C.H0:β1≠β2≠0;H1:β1=β2≠0
D.H0:β1=β2=0;H1:β1至少有一个不为零
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下
请根据上述结果,从下列备选答案中选出正确答案。
对于多元线性回归模型,以下假设中正确的有()。A.因变量与自变量之间的关系为线性关系
B.随机误差项的均值为1
C.随机误差项之间是不独立的
D.随机误差项的方差是常数
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
请根据上述结果,从下列备选答案中选出正确答案。
根据样本观测值和估计值计算回归系数β2的t统计量,其值为f=8.925,根据显著性水平(α=0.05)与自由度,由t分布表查得t分布的右侧临界值为2.431,因此,可以得出的结论有()。A.接受原假设,拒绝备择假设
B.拒绝原假设,接受备择假设
C.在95%的置信水平下,图.png是由β2 =0这样的总体产生的
D.在95%的置信水平下,居住面积对居民家庭电力消耗量的影响是显著的
考题
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:
表 1 回归方程的输出结果
描述城镇居民家庭人均食品消费支出与城镇居民家庭人均可支配收入之间关系适合的图形是( )。A.直方图
B.折线图
C.散点图
D.雷达图
考题
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:
表 1 回归方程的输出结果
根据表1~表3的输出结果可以得出( )。A.回归方程为:
B.城镇居民家庭人均食品消费支出与城镇居民家庭人均可支配收入和食品类居民消费价格指数的总体相关程度为87.7%
C.多元回归分析中拟合优度大小应根据判定系数( )来衡量
D.多元回归分析中拟合优度大小应根据调整后的判定系数( )来衡量
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
请根据上述结果,从下列备选答案中选出正确答案。
检验回归方程是否显著,正确的假设是()。
A.H0: β1 =β2 =0;H1: β1≠β2 ≠0
B.H0: β1 =β2 ≠0;H1: β1≠β2 =0
C.H0: β1 ≠β2 ≠0;H1: β1=β2 ≠0
D.H0: β1 =β2 =0;H1: β1至少有一个不为零
考题
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:
表 1 回归方程的输出结果
城镇居民家庭人均食品消费支出、城镇居民家庭人均可支配收入和食品类居民消费价格指数数据属于( )。A.一手数据
B.二手数据
C.实验数据
D.定性数据
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
请根据上述结果,从下列备选答案中选出正确答案。
回归系数β2=0.2562的经济意义为()。
A.我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0. 2562千瓦小时
B.在可支配收入不变的情况下,我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
C.在可支配收入不变的情况下,我国居民家庭居住面积每减少1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
D.我国居民家庭居住面积每增加l平方米,居民家庭电力消耗量平均减少0.2562千瓦小时
考题
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:
表 1 回归方程的输出结果
如果 ,根据表2,下列说法正确的是( )。A.F检验的假设为:
B.F检验的假设为:
C.回归方程的线性关系显著
D.回归方程的线性关系不显著
考题
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:
表 1 回归方程的输出结果
如果 ,根据表3,下列说法正确的是( )。A.城镇居民家庭人均可支配收入对城镇居民家庭人均食品消费支出的线性关系 显著
B.城镇居民家庭人均可支配收入对城镇居民家庭人均食品消费支出的线性关系不显著
C.食品类居民消费价格指数对城镇居民家庭人均食品消费支出的线性关系显著
D.食品类居民消费价格指数对城镇居民家庭人均食品消费支出的线性关系不显著
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
请根据上述结果,从下列备选答案中选出正确答案。
对于多元线性回归模型,以下假设中正确的有()。
A.因变量与自变量之间的关系为线性关系
B.随机误差项的均值为1
C.随机误差项之间是不独立的
D.随机误差项的方差是常数
考题
根据下面资料,回答79-82题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(Y,单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
据此回答以下题目。
回归系数β2的经济意义为( )A.我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
B.在可支配收入不变的情况下,我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
C.在可支配收入不变的情况下,我国居民家庭居住面积每减少1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
D.我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均减少0.2562.千瓦小时
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(Y,单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
根据样本观测值和估计值计算回归系数β2的t统计量,其值为t=8.925,根据显著性水平(a=0.05)与自由度,由t分布表查得t分布的右侧临界值为2.431,因此,可以得出的结论有( )。
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(Y,单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
检验回归方程是否显著,正确的假设是()。
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(Y,单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
根据上述回归方程式计算的多重判定系数为0.9235,其正确的含义是( )。A.在Y的总变差中,有92.35%可以由解释变量X1和X2解释
B.在Y的总变差中,有92.35%可以由解释变量X1解释
C.在Y的总变差中,有92.35%可以由解释变量X2解释
D.在Y的变化中,有92.35%是由解释变量X1和X2决定的
考题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(Y,单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
回归系数β2的经济意义为()。A.我国居民家庭居住面积每增加l平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
B.在可支配收入不变的情况下,我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
C.在可支配收入不变的情况下,我国居民家庭居住面积每减少1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
D.我国居民家庭居住面积每增加l平方米,居民家庭电力消耗量平均减少0.2562千瓦小时
考题
为预测我国居民对电子表的需求量,定义变量“商品价格”(x1,单位:元/件)、“消费者人均月收入”(x2,单位:元)及“商品需求量”(y,单位:件),建立多元线性回归方程如下:y=4990.519-35.66597x1+6.19273x2,请根据上述结果,从备选答案中选出正确答案。根据计算上述回归方程式的多重判定系数为0.9540,其正确的含义是()。A、在Y的变化中,有95.40%是由解释变量x1和x2决定的B、在Y的总变差中,有95.40%可以由解释变量x2解释C、在Y的总变差中,有95.40%可以由解释变量x1解释D、在Y的总变差中,有95.40%可以由解释变量x1和x2解释
考题
不定项题A我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0. 256 2千瓦小时B在可支配收入不变的情况下,我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0. 256 2千瓦小时C在可支配收入不变的情况下,我国居民家庭居住面积每减少1平方米,居民家庭电力消耗量平均增加0. 256 2千瓦小时D我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均减少0. 256 2千瓦小时
考题
多选题回归系数β2=0.2562的经济意义为( )。A我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时B在其他条件不变的情况下,我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时C在其他条件不变的情况下,我国居民家庭居住面积每减少1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时D我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均减少0.2562千瓦小时
热门标签
最新试卷