网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
己知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P1=20元和P2= 30元,该消费者的效用函数为
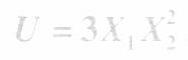
该消费者每年购买这两种商品的数量应各是多少每年从中获得的总效用是多少?
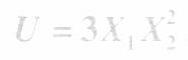
该消费者每年购买这两种商品的数量应各是多少每年从中获得的总效用是多少?
参考答案
参考解析
解析:已知U =3X1X2,又根据消费者的效用最大化的均衡条件为
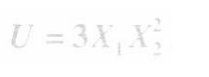
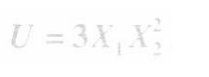
更多 “己知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P1=20元和P2= 30元,该消费者的效用函数为 该消费者每年购买这两种商品的数量应各是多少每年从中获得的总效用是多少?” 相关考题
考题
假设某消费者的均衡如图所示。其中,横轴OX1和纵轴OX2分别表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U为消费者的无差异曲线,E点为效用最大化的均衡点已知商品1的价格P1=2元。(1)求消费者的收入;(2)求商品2的价格P2;(3)写出预算线方程;(4)求预算线的斜率;(5)求E点的MRS12的值。
考题
已知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P1=20元和P2=30元,该消费者的效用函数为U=3X1X22,该消费者每年购买这两种商品的数量各应是多少?每年从中获得总效用是多少?
考题
消费者显示了对于商品1和商品2的如下需求: 价格为(p1,p2)=(2,4)时,需求为(q1,q2)-(1,2);价格为(p1,p2)=(6,3)时,需求为(q1,q2)一(2,1)。该消费者的选择是与其效用最大化目标一致的。
考题
某消费者对商品x和商品y的效用函数为u(x,y)=x-0.5x2+y。商品x的价格为p,商品y的价格标准化为1。问题:假定商品x由一个具有规模报酬不变生产技术的垄断厂商提供,单位成本为0.4元。求产品定价、消费者剩余、生产者剩余。
考题
假定某消费者的效用函数为U=q^0.5+3M,其中,q为某商品的消费量,M为收入。 求:(1)该消费者的需求函数;(2)该消费者关于该商品的反需求函数;(3)当p=1/12、q=4时的消费者剩余。
考题
m为收入,P1,P2分别为商品1和2的价格,当m>P2时,商品1和商品2的需求方程分别为X1 =
假设横轴表示商品1的数量,纵轴表示商品2的数量,p1=1,P2 =2,当m>2时,收入提供曲线为( )。A.一条垂直线
B.一条水平线
C.一条斜率为2的直线
D.一条斜率为1/2的直线
考题
设某消费者的效用函数为柯布-道格拉斯类型的,即U=x^αy^β,商品x和商品y的价格分别为Px和Py,消费者收入为M,α和β为常数切α+β=1 (1)求该消费者关于商品x和商品y的需求函数。 (2)证明:当商品x和y的价格及消费者的收入均以相同的比例变化时,消费者对两商品的需求关系维持不变; (3)证明:该消费者效用函数中的参数α和β分别为商品x和商品y的消费支出占消费者收入的份额。
考题
某消费者的效用函数为U=(x1,x2)=x11/3x2/3,x1和x2分别为两种商品的消费量,消费者收入为100,两种商品现在价格分别为P1=1,P2=2,求: 如果第一种商品价格由1提高为2,其他因素不变,则价格上升对第一种商品的消费量影响的总效应有多少?按照Slutsky分解原理,收入效应和替代效应分别是多少?
考题
设某消费者的效用函数为柯布一道格拉斯类型的,即
商品x和商品y的价格分别为
消费者的收人为M,a和β为常数,且a+ β=1。 (1)求该消费者关于商品X和商品y的需求函数。 (2)证明当商品X和商品y的价格以及消费者的收入同时变动一个比例时,消费者对两商品的需求关系维持不变。 (3)证明消费者效用函数中的参数a和β分别为商品x和商品y的消费支出占消费者收入的份额。
考题
某消费者的效用函数
消费者的收人为M。 (1)请画出该消费者的无差异曲线。 (2)画出相应的收入消费曲线(ICC)、价格消费曲线(PCC)和恩格尔曲线(EC)。 (3)求商品X2的需求函数:X2 (Pl,P2,M)。 (4)已知M=100,
求效用最大化的商品组合。
考题
某消费者的效用函数为U=(x1,x2)=x11/3x2/3,x1和x2分别为两种商品的消费量,消费者收入为100,两种商品现在价格分别为P1=1,P2=2,求: 计算第一种商品价格从1变化为2,要保持原有效应不变的收入补偿数额。
考题
已知某消费者的效用函数为U=X1X2,两商品的价格分别为P1=4、P2=2,消费者的收入是M=80.现在假定商品1的价格下降为P1=2.求: (1)由商品1的价格P1下降导致的总效应,使得该消费者对商品1的购买量发生多少变化? (2)由商品1的价格P1下降导致的替代效应,使得该消费者对商品1的购买量发生多少变化? (3)由商品1的价格P1下降导致的收入效应,使得该消费者对商品1的购买量发生多少变化?
考题
假设在一个2×2的交换经济中消费者A和B交换两种商品z和y,消费者A的效用函数 是UA (XA,yA)=
,消费者B的效用函数是ub(xb,yB)=
他们拥有两种商品的初始 禀赋分别是WA(40,60)和WB(40,40)。标准化商品x的价格Px=1,商品y的价格为P。 (1)计算消费者A和B对两种商品z和y的需求函数。 (2)计算该交换经济的均衡价格及均衡配置。
考题
某消费者对商品x和商品y的效用函数为u(x,y)=x-0.5x2+y。商品x的价格为p,商品y的价格标准化为1。问题:若x由两个厂商供给,单个产品成本为0.4,两个厂商之间进行古诺竞争,求均衡时的市场定价、生产者剩余和消费者剩余
考题
某消费者的效用函数为u(x1.x2)一√五云,商品x1和x2的价格为P1和P2,收入为ya (1)假设商品x1和x2的价格为P1=l和P2=2,该消费者收入为y=100。求该消费者对两种商 品的需求量。 (2)若商品x1价格升至2,即此时P1=P2 =2,该消费者收入不变。求此价格变化对商品Xl产生的替代效应和收入效应。
考题
某消费者的效用函数为U=(x1,x2)=x11/3x2/3,x1和x2分别为两种商品的消费量,消费者收入为100,两种商品现在价格分别为P1=1,P2=2,求: 消费者最优消费的xi和xo量。
考题
假设消费者用既定的收入w购买两种商品,P1和P2分别为两种商品的既定价格,以Q1和Q2分别表示两种商品的数量,则P1Q1+P2Q2=w;MU1和MU2分别表示两种商品的边际效用,λ表示每一元货币带来的边际效用,则消费者效用最大化的均衡条件为( )。
A.MU1/P2=MU2/P1=λ
B.MU1/P1=MU2/P2=λ
C.P1/MU1=P2/MU2=λ
D.P2/MU1=P1/MU2=λ
考题
若消费者张某消费X和Y两种商品的效用函数U=X2Y2 ,张某收入为500元,X和Y的价格分别为PX =2元,PY=5元,求: (1)张某的消费均衡组合点。 (2)若政府给予消费者消费X以价格补贴,即消费者可以原价格的50%购买X,则张某将消费X和Y各多少? (3)若某工会愿意接纳张某为会员,会费为100元,但张某可以50%的价格购买X,则张某是否应该加入该工会?
考题
问答题令某消费者的收入为M,两种商品的价格为P1、P2。如果该消费者的无差异曲线是线性的,且斜率为-a,求:该消费者的最优商品组合。
热门标签
最新试卷