网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
某人的效用函数为
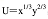
收入为m,其中x和y的价格分别为p1,p2。求该消费者的间接效用函数。
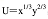
收入为m,其中x和y的价格分别为p1,p2。求该消费者的间接效用函数。
参考答案
参考解析
解析: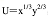
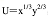
更多 “某人的效用函数为 收入为m,其中x和y的价格分别为p1,p2。求该消费者的间接效用函数。” 相关考题
考题
计算题:假定X和Y两种商品的效用函数为U=
计算题:假定X和Y两种商品的效用函数为U=,要求:(1)若X=5,则在总效用为10单位的无差异曲线上,对应的Y应为多少?这一商品组合对应的边际替代率是多少?(2)计算上述效用函数对应的边际替代率。
考题
总效用是指消费者在一定时间内从一定数量的商品的消费中所得到的______。总效用函数为:______。边际效用是指消费者在一定时间内增加一单位商品的消费所得到的效用量的______。边际效用函数为:______。
考题
某人的效用函数为U(C,R) =C-(12 -R)2,其中R是他每天拥有的闲暇时间,C为消费量。他每天有16小时可用在工作和闲暇上,每天有20元的非劳动收入。消费品的价格是每单位1元。工资为每小时10元,他将选择多少小时进行工作以获得最大效用?
考题
已知某人的效用函数为TU=4X+Y,如果消费者消费16单位X和14单位Y,试求: (1)消费者的总效用 (2)如果因某种原因消费者只能消费4个单位X产品,在保持总效用不变的情况下,需要消费多少单位Y产品?
考题
多选题尽管期望效用决策标准具有明显的优点,但在实施时也会出现一些困难,表现在:()。A在大型组织中,使用谁的效用函数B假设已经解决了使用谁的效用函数的问题,但在衡量个人效用函数时还会产生更大的困难C当人们力求从经验中导出一个效用函数时,所使用的方法有时会形成不一致的效用评价D导出效用函数的理论方法也不一定会产生满意的结果E不同个人的效用函数是不能直接比较的,因此在理论上不可能形成一个集体的效用函数
考题
问答题已知某人的效用函数为TU=4X+Y,如果消费者消费16单位X和14单位Y,试求: (1)消费者的总效用 (2)如果因某种原因消费者只能消费4个单位X产品,在保持总效用不变的情况下,需要消费多少单位Y产品?
考题
问答题设某人拥有的财富为w,其效用函数形式为u(w)=1/w,他面对如下一个彩票:以概率p得到w1,以概率1-p得到w2,他需要拥有多少财富w使得他接受这个彩票和保持现有财富是无差异的。
考题
单选题某人拥有资本ω,他的效用函数为lnx,该人面临的潜在损失随机变量为X,X的分布列为P(X=0)=P(X=16)=0.5,若该投资者将潜在损失的50%进行了保险,他愿意支付的最高保费为5,则该投资者的初始资本ω=( )。A
23 B
33 C
35 D
36 E
14
热门标签
最新试卷