网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
阅读以下说明和流程图，回答问题1和问题2。
【说明】
设8位二进制代码B0B1…B7中的最高位B0为奇偶校验位。对于任何给定的代码
B1B2…B7，可按下式计算偶校验位：
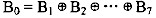
其中，“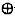
”表示“异或”运算。
下面的流程图描述了计算偶校验位的过程。
【流程图】
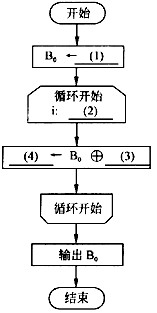
注：流程图中，循环开始的说明按照“循环变量名：循环初值，循环终值，增量”格式描述。
将流程图中的(1)～(4)处补充完整。
参考答案
更多 “ 阅读以下说明和流程图，回答问题1和问题2。【说明】设8位二进制代码B0B1…B7中的最高位B0为奇偶校验位。对于任何给定的代码B1B2…B7，可按下式计算偶校验位：其中，“”表示“异或”运算。下面的流程图描述了计算偶校验位的过程。【流程图】注：流程图中，循环开始的说明按照“循环变量名：循环初值，循环终值，增量”格式描述。将流程图中的(1)～(4)处补充完整。 ” 相关考题
考题
阅读以下说明和流程图，回答问题1～2，将解答填入对应的解答栏内。[说明]下面的流程图描述了计算自然数1到N(N≥1)之和的过程。[流程图][问题1] 将流程图中的(1)～(3)处补充完整。[问题2] 为使流程图能计算并输出1*3+2*4+…+N*(N+2)的值，A框内应填写(4)；为使流程图能计算并输出不大于N的全体奇数之和，B框内应填写(5)。
考题
阅读下列说明和流程图2-3，将应填入(n)的字句写在答题纸的对应栏内。【说明】下面的流程图描述了对8位二进制整数求补的算法。该算法的计算过程如下：从二进制数的低位(最右位)开始，依次向高位逐位查看，直到首次遇到“1”时，停止查看。然后，对该“1”位左面的更高位(如果有的话)，逐位求反，所得的结果就是对原二进制数求补的结果。例如：对二进制整数10101000求补的结果是01011000。设8位二进制整数中的各位，从低位到高位，依次存放在整型数组BIT的B1T[1]～BIT[8]中。例如，二进制整数10101000存放在数组BIT后，就有BIT[1]=0，BIT[2]=0，…，BIT[7] =0，BIT[8]=1。若流程图中存在空操作，则用NOP表示。【流程图】注：流程图中(1)处按“循环变量名：循环初值，增量，循环终值”格式描述。
考题
关于奇偶校验码,以下说法不正确的是___________。
a.字节"10000110”码的奇校验位为"0”b.字节"11100110”码的偶校验位为"1”c.奇偶校验码能够发现一个字节中任意多位出错d.奇偶校验码通常为1个字节补充1个二进制位，称为校验位，通过设置校验位的值为"1”或"0”，使这个字节和校验位的"1”的个数为奇数或偶数
考题
阅读下列说明和流程图，将应填入(n)的语句写在对应栏内。【流程图】下面的流程图描述了对16位二进制整数求补的算法。计算过程是：从二进制数的低位 (最右位)开始，依次向高位逐位查看，直到首次遇到“1”时，停止查看。然后，对该“1”位左面的更高位(如果有的话)，逐位求反，所得的结果就是对原二进制数求补的结果。例如：对二进制整数10111001 10101000求补的结果是01000110 01011000。设16位二进制整数中的各位，从低位到高位，依次存放在整型数组BIT的BIT[1]～BIT[16]中。例如，二进制整数10111001 10101000存放在数组BIT后，就有BIT1[1]=0， BIT[2]=0，……，BIT[15]=0，BIT[16]=1。流程图(如图1所示)中(1)处按“循环变量名：循环初值，增量，循环终值”格式描述。若流程图中存在空操作，则用NOP表示。
考题
阅读以下说明和流程图，回答问题1-2，将解答填入对应的解答栏内。[说明]下面的流程图采用欧几里得算法，实现了计算两正整数最大公约数的功能。给定正整数m和 n，假定m大于等于n，算法的主要步骤为：(1)以n除m并令r为所得的余数；(2)若r等于0，算法结束；n即为所求；(3)将n和r分别赋给m和n，返回步骤(1)。[流程图][问题1] 将流程图中的(1)～(4)处补充完整。[问题2] 若输入的m和n分别为27和21，则A中循环体被执行的次数是(5)。
考题
阅读以下说明和流程图，回答问题将解答填入对应栏。[说明]下面的流程图，用来完成计算一组数组中的中值，其方法是：将数组中的一个值与其他值比较，并计算大于等于被比较数的数值的个数，以及小于等于被比较数的数值的个数，如果两数都大于n/2，则已经找到了中值，否则继续之前的步骤。注：流程中循环开始的说明按照“循环变量：循环初值，循环终值，增量”格式描述；[问题]将流程图的(1)～(5)处补充完整。
考题
●试题一阅读下列说明和流程图，将应填入(n)的语句写在答题纸的对应栏内。【流程图】图1下面的流程图描述了对16位二进制整数求补的算法。计算过程是：从二进制数的低位(最右位)开始，依次向高位逐位查看，直到首次遇到"1"时，停止查看。然后，对该"1"位左面的更高位(如果有的话)，逐位求反，所得的结果就是对原二进制数求补的结果。例如：对二进制整数10111001 10101000求补的结果是01000110 01011000。设16位二进制整数中的各位，从低位到高位，依次存放在整型数组BIT的BIT［1］～BIT［16］中。例如，二进制整数10111001 10101000存放在数组BIT后，就有BIT1［1］=0，BIT［2］=0，……，BIT［15］=0，BIT［16］=1。流程图(如图1所示)中 (1) 处按"循环变量名：循环初值，增量，循环终值"格式描述。若流程图中存在空操作，则用NOP表示。
热门标签
最新试卷