网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
阅读以下说明和流程图,填补流程图中的空缺(1)一(5),将解答填入答题纸的对应栏内。
【说明】
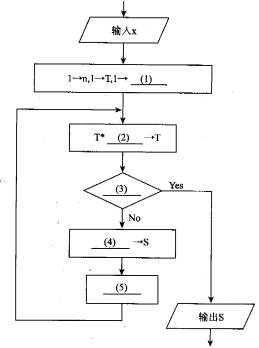
下面的流程图采用公式ex=1+x+x2/2 1+x3/3 1+x4/4 1+…+xn/n!+???计算ex的近似值。设x位于区间(0,1),该流程图的算法要点是逐步累积计算每项xx/n!的值(作为T),再逐步累加T值得到所需的结果s。当T值小于10-5时,结束计算。
【流程图】
参考答案
更多 “ 阅读以下说明和流程图,填补流程图中的空缺(1)一(5),将解答填入答题纸的对应栏内。【说明】下面的流程图采用公式ex=1+x+x2/2 1+x3/3 1+x4/4 1+…+xn/n!+???计算ex的近似值。设x位于区间(0,1),该流程图的算法要点是逐步累积计算每项xx/n!的值(作为T),再逐步累加T值得到所需的结果s。当T值小于10-5时,结束计算。【流程图】 ” 相关考题
考题
阅读以下说明和流程图,回答问题1~2,将解答填入对应的解答栏内。[说明]下面的流程图描述了计算自然数1到N(N≥1)之和的过程。[流程图][问题1] 将流程图中的(1)~(3)处补充完整。[问题2] 为使流程图能计算并输出1*3+2*4+…+N*(N+2)的值,A框内应填写(4);为使流程图能计算并输出不大于N的全体奇数之和,B框内应填写(5)。
考题
阅读下列说明和流程图,将应填入(n)的字句写在对应栏内。【说明】下列流程图(如图4所示)用泰勒(Taylor)展开式sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x2n+1/(2n+1)!+…【流程图】计算并打印sinx的近似值。其中用ε(>0)表示误差要求。
考题
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。【说明】下列流程图用泰勒(Taylor)展开式y=ex=1+x+x2/2!+x3/3!+…+xn/n!+…计算并打印ex的近似值,其中用ε(>0)表示误差要求。【流程图】
考题
?????? 阅读以下说明和流程图,填补流程图中的空缺(1)~(5),将解答填入答题纸的对应栏内。【说明】本流程图旨在统计一本电子书中各个关键词出现的次数。假设已经对该书从头到尾依次分离出各个关键词{A(i)li=l,…,n}(n>1)}.其中包含了很多重复项,经下面的流程处理后,从中挑选出所有不同的关键词共m个{K(j)[j=l,…,m},而每个关键词K(j)出现的次数为NK(j).j=l,…,m。??????
考题
●试题一阅读下列说明和流程图,将应填入(n)的字句写在答题纸的对应栏内。【说明】下列流程图(如图4所示)用泰勒(Taylor)展开式sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x 2n+1/(2n+1)!+…【流程图】图4计算并打印sinx的近似值。其中用ε(0)表示误差要求。
考题
试题一(共 15 分)阅读以下说明和流程图,填补流程图中的空缺(1)~(9) ,将解答填入答题纸的对应栏内。[说明]假设数组 A 中的各元素 A(1),A(2) ,…,A(M)已经按从小到大排序(M≥1) ;数组 B 中的各元素 B(1),B(2),…,B(N)也已经按从小到大排序(N≥1) 。执行下面的流程图后, 可以将数组 A 与数组 B 中所有的元素全都存入数组 C 中, 且按从小到大排序 (注意:序列中相同的数全部保留并不计排列顺序) 。例如,设数组 A 中有元素:2,5,6,7,9;数组B 中有元素:2,3,4,7;则数组 C 中将有元素:2,2,3,4,5,6,7,7,9。[流程图]
考题
阅读说明和流程图,填补流程图中的空缺(1)?(5),将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1,a2=1,…,an=an-1+an-2!n=3,4,…}的前n项(n>=2) 之和S。例如,菲波那契数列前6项之和为20。计算过程中,当前项之前的两项分别动态地保存在变量A和B中。【流程图】
考题
第一题 阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。
【说明】
对于大于1的正整数n,(x+1)n可展开为
问题:1.1 【流程图】
注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1。
格式为:循环控制变量=初值,终值,递增值。
考题
阅读以下说明和流程图,填写流程图中的空缺,将解答填入答题纸的对应栏内。【说明】设[a1b1],[a2b2],...[anbn]是数轴上从左到右排列的n个互不重叠的区间(a1
热门标签
最新试卷