网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
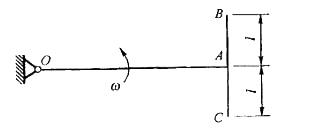
T形均质杆OABC以匀角速度ω绕O轴转动,如图所示。已知OA杆的质量为2m,长为2l,BC杆质量为m,长为l,则T形杆在该位置对O轴的动量矩为:



参考答案
参考解析
解析:提示:动量矩 LO=JOω,其中JO=JO(OA)+ JO(BC)。
更多 “T形均质杆OABC以匀角速度ω绕O轴转动,如图所示。已知OA杆的质量为2m,长为2l,BC杆质量为m,长为l,则T形杆在该位置对O轴的动量矩为: ” 相关考题
考题
一均质杆AB,长为L,质量为m,以角速度ω绕O轴转动,则杆对过O点的Z轴的动量矩LZ大小为()。A.LZ=1/12mL2ωB.LZ=1/3mL2ωC.LZ=7/48mL2ωD.LZ=1/4mL2ω
考题
匀质杆质量为m,长OA=l,在铅垂面内绕定轴o转动。杆质心C处连接刚度系数是较大的弹簧,弹簧另端固定。图示位置为弹簧原长,当杆由此位置逆时针方向转动时,杆上A点的速度为VA,若杆落至水平位置的角速度为零,则vA的大小应为:
考题
如图所示,曲柄OA长R,以匀角速度ω绕O轴转动,均质圆轮B在水平面上做纯滚动,其质量为m,半径为r。在图示瞬时,OA杆铅直。圆轮B对接触点C的动量矩为( )mRrω。
A.0.5
B.1.0
C.1.5
D.2.0
考题
均质细直杆OA长为l,质量为m,A端固结一质量为m的小球(不计尺寸),如图4-76所示。当OA杆以匀角速度ω绕O轴转动时,该系统对O轴的动量矩为()。
A. 1/3ml2ω B. 2/3ml2ω C. ml2ω D. 4/3ml2ω
考题
均质细直杆AB长为l,质量为m,以匀角速度ω绕O轴转动,如图4-69所示, 则AB杆的动能为( )。
热门标签
最新试卷