网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
在一元线性回归分析中，根据数据(xi,yi),已知：Lxx=10, Lxy=8,以下计算正确的有 ( )。
A.总平方和ST= 5. 5 B.回归平方和SR =6.4
C. r = 1. 25 D.b=0. 8
E.残差平方和SE=7
A.总平方和ST= 5. 5 B.回归平方和SR =6.4
C. r = 1. 25 D.b=0. 8
E.残差平方和SE=7
参考答案
参考解析
解析：回归方程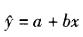
，b = Lxy/Lxx = 0. 8 ；回归平方和SR=bLxy=6. 4。
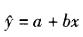，b = Lxy/Lxx = 0. 8 ；回归平方和SR=bLxy=6. 4。
更多 “在一元线性回归分析中，根据数据(xi,yi),已知：Lxx=10, Lxy=8,以下计算正确的有 ( )。 A.总平方和ST= 5. 5 B.回归平方和SR =6.4 C. r = 1. 25 D.b=0. 8 E.残差平方和SE=7” 相关考题
考题
由12对观测值(xi，yi)，i=1，2，…，12，求得Lxx=238，Lyy=106，Lxy=-153，则下列叙述正确的有( )。A．x与y的相关系数为0.963B．x与y的相关系数为-0.963C．y对x的一元线性回归系数为-1.443D．y对x的一元线性回归系数为-0.643E．x对y的一元线性回归系数为-0.643
考题
在一元线性回归分析中，根据数据(xi，yi)，已知：Lxx=10，Lxy=8，以下计算正确的有( )。A．总平方和ST=5.5B．回归平方和SR=6.4C．r=1.25D．b=0.8E．残差平方和SE=7
考题
由l5对数据(xi，yi)，i=1，2，…，15，算得Lxx=355，Lyy=3102，Lxy=－923，贝0回归方程y=a+bx中回归系数b=（ ）。A.1.7B.－l.7C.2.6D.－2.6
考题
由n个数组(xi，yi。)计算得 Lxx=330，Lxy=-l68，Lyy=9.4 由此可以看出（ ）。A.x与y，的相关系数r0B.x与Y的相关系r0C.Y对x的回归系数b0D.y对x的回归系数b0E.相关系数r与回归系数异号
考题
若收集了n组数据(xi，yi)，i=1，2，…，n，并求得Lxx=330，Lxy=168，如Lyy= 88.9，则一元线性回归方程(作图)中的b=( )。A．0.5091B．0.5292C．1.8898D．1.9643
考题
若收集了n组数据(xi,yi), i =1， 2，…n，并求得Lxx=330，Lxy=168，Lyy=88.9，则一元线性回归方程中的b=( )。
A. 0.5091 B. 0.5292 C. 1. 8898 D. 1.9643
考题
在变量Y表示对X进行回归分析时，根据10对观测值(xi,yi), i =1， 2，…10，算得如下结果：，Lxx=336，Lxy=131.25，Lyy=168。
请回答下列问题。
回归方程中的常数项a为（ ）。
A. -19.6 B. -2.6 C. 2.6 D. 26
考题
由 10 对观测值（xi，yi)，i＝1，…，10，求得 Lxx＝196，Lyy＝144，Lxy＝142，则下列计算结果中，正确的有（ ）。
A.相关系数为0. 845 2 B.相关系数为0. 724 5
C.相关系数为﹣0.845 2 D. y对的回归系数为0. 9861
E. y对x的回归系数为0.724 5
考题
由n个数组（xi，yi)计算得Lxx= 330，_Lxy=﹣168，Lyy= 9.4由此可以看出（ ）。
A. x与y的相关系数r>0
B.工与y的相关系数r
C. y对x的回归系数b>0
D. y对x的冋归系数b
E.相关系数r与回归系数b异号
考题
在变量Y表示对X进行回归分析时，根据10对观测值(xi,yi), i =1， 2，…10，算得如下结果：，Lxx=336，Lxy=131.25，Lyy=168。
请回答下列问题。
X与Y的样本相关系数r为（ ）。
A. -0.8 B. 0.8 C. 0.64 D. 0.5
考题
在变量Y表示对X进行回归分析时，根据10对观测值(xi,yi), i =1， 2，…10，算得如下结果：，Lxx=336，Lxy=131.25，Lyy=168。
请回答下列问题。
Y对X的回归系数b为（ ）。
A. 0.5 B. -0.5 C. 0.582 D. -0.582
考题
在变量Y表示对X进行回归分析时，根据10对观测值(xi,yi), i =1， 2，…10，算得如下结果：，Lxx=336，Lxy=131.25，Lyy=168。
请回答下列问题。
当x0=20时，预测为（ ）。
A. 12.6 B. 9.6 C. -7.4 D. 29.6
考题
由 15 对数据（xi，yi),= 1, 2，…，15，算得 Lxx= 355，Lyy = 3102, Lxy =— 923，则回归方程中回归系数b=( )。
A. 1.7 B. —1.7
C. 2. 6 D. —2. 6
考题
由 12 对数据 （xi，yi）,i = 1，2,…，12，算得 Lxx=165，Lyy=372, Lxy=﹣232，则X与Y间的相关系数r为（ ）。
A. 0. 936 B. ﹣0. 936
C. 0.875 D. ﹣0. 875
考题
由 10 对观测值 (xi,yi),i=1，2,…，10，计算得Lxx= 160，Lxy=－216，Lyy =﹣360,则样本相关系数r=( )。
A. 0. 90 B. 0. 85
C. ﹣0. 85 D. ﹣0. 90
考题
由n个数组(xi,yi)计算得Lxx= 330, Lxy =-168,Lxy=9.4由此可以看出（）。
A. X与y，的相关系数r>0
B. X与y的相关系数rC. y与x对r的回归系数b>0
D. y对x的回归系数bE.相关系数r与回归系数异号
考题
某地区2002～2013年统计某种产品消费量(Y)及同期相关产业产值(X)得出如下数据：∑xi2=28.68∑yi=80.4，=8.94∑xi=16.2，=1.62∑xiyi=154.33，用一元线性回归模型的回归系数是（ ）。A、9.89B、-7.55C、3.44D、-2.77
考题
通过最小二乘估计，得到某地区某种钢板消费量(Y)与同期第二产业产值(X)的一元线性回归方程为y=-7.55+9.59x，经计算∑(yi-yi’)2=11.87，∑(xi-x)2=1.56，取α=0.05，对其进行t检验，结论是（ ）。(已知t(0.05,8)=1.86;t(0.025,8)=2.36，n=10)A、tb大于1.86，线性假设合理B、tb大于1.86，线性假设不合理C、tb大于2.36，线性假设合理D、tb大于2.36，线性假设不合理
考题
采用最小二乘法确定回归方程Y=ax+b的常数项正确的计算公式是（）A、b=Lxy/Lxx，a=y平-bx平B、b=Lxx/Lxy，a=y平-bx平C、b=Lxy/Lxx，a=y-bxD、b=Lxx/Lxy，a=y-bx
考题
单选题一元线性回归模型的总体回归直线可表示为（ ）。A
E（yi）＝α＋βxiB
y(∧)i＝α(∧)＋β(∧)xiC
y(∧)i＝α(∧)＋β(∧)xi＋eiD
y(∧)i＝α＋βxi＋μi
考题
单选题在对两个变量x，y进行线性回归分析时，有下列步骤： ①对所求出的回归直线方程作出解释； ②收集数据（xi，yi），1，i=2，…，n； ③求线性回归方程； ④求未知参数； ⑤根据所搜集的数据绘制散点图 如果根据可行性要求能够作出变量x，y具有线性相关结论，则在下列操作中正确的是（）A
①②⑤③④B
③②④⑤①C
②④③①⑤D
②⑤④③①
考题
单选题采用最小二乘法确定回归方程Y＝ax＋b的常数项，正确的计算公式是（）。A
b＝LXY/LXX，a＝－bB
b＝LXX/LXY，a＝－bC
b＝LXY/LXX，a＝y－bxD
b＝LXX/LXY，a＝y－bx
考题
单选题一元线性回归模型的总体回归直线可表示为（ ）。[2016年5月真题]A
E（yi）＝α＋βxiB
y(∧)i＝α(∧)＋β(∧)xiC
yi＝α(∧)＋β(∧)xi＋eiD
yi＝α＋βxi＋mi
热门标签
最新试卷