网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
用克拉默法则解线性方程组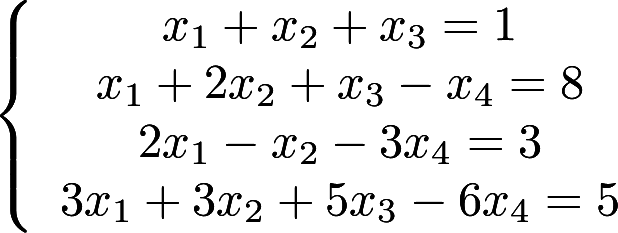

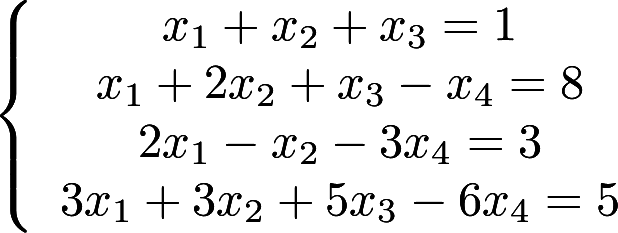
参考答案

参考解析
解析：
更多 “用克拉默法则解线性方程组” 相关考题
考题 设n元齐次线性方程组AX=O只有零解,则秩(A)=()。
查看答案
考题 若r(A,b)=4,r(A)=3,则线性方程组AX=b解的情况是()。
查看答案
考题 用迭代法解线性方程组时，迭代能否收敛与初始向量的选择、系数矩阵及其演变方式有关，与常数项无关。()
查看答案
考题 非齐次线性方程组任意两个解之差为对应系数的齐次线性方程组的解。()
查看答案
考题 用高斯顺序消去法解线性方程组，消元能进行到底的充分必要条件是线性方程组的系数矩阵的各阶顺序主子式均不为0()
查看答案
考题 用列主元消去法解线性方程组,A、3B、4C、-4D、9
查看答案
考题 设A为矩阵，都是线性方程组Ax=0的解，则矩阵A为：
查看答案
考题 齐次线性方程组AX=0若有两个不同的解，它就有无穷多个解
查看答案
考题 给定线性方程组 则其解的情况正确的是（　　）。A．有无穷多个解 B．有唯一解 C．有多于1个的有限个解 D．无解
查看答案
考题 都是线性方程组Ax=0的解，则矩阵A为:
查看答案
考题 解线性方程组其中 .
查看答案
考题 用克拉默法则解方程组
查看答案
考题 求齐次线性方程组的基础解系
查看答案
考题 解齐次线性方程组：
查看答案
考题 解非齐次线性方程组
查看答案
考题 已知齐次线性方程组 同解，求a，b，c的值.
查看答案
考题 已知下列非齐次线性方程组(Ⅰ)，(Ⅱ) 　　 　　(1)求解方程组(Ⅰ)，用其导出组的基础解系表示通解. 　　(2)当方程组中的参数m，n，t为何值时，方程组(Ⅰ)与(Ⅱ)同解.
查看答案
考题 求出一个齐次线性方程组，使它的基础解系由向量组成
查看答案
考题 设线性方程组与方程有公共解，求a的值及所有公共解
查看答案
考题 设线性方程组(I)与(II)有公共的非零解,其中(I)为，(II)有基础解系，求p,t的值和全部公共解
查看答案
考题 设线性方程组问方程组何时无解，有唯一解，有无穷多解，有无穷多解时，求出其全部解。
查看答案
考题 设，，已知线性方程组存在两个不同的解.
查看答案
考题 求齐次线性方程组的全部解（要求用基础解系表示）。
查看答案
考题 齐次线性方程组的基础解系为（ ）。
查看答案
考题 单选题用列主元消去法解线性方程组 ，第1次消元，选择主元为（） 。A -4B 3C 4D -9
查看答案
热门标签
最新试卷