网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
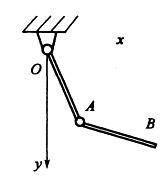
在图示定平面Oxy内，杆OA可绕轴O转动，杆AB在点A与杆OA铰接，即杆AB可绕点A转动。该系统称为双摆，其自由度数为：

A.1个
B.2个
C.3个
D.4个

参考答案

参考解析
解析：在平面内自由运动的两杆件应有6个自由度，而0、A处有4个约束。
答案:B
更多 “在图示定平面Oxy内，杆OA可绕轴O转动，杆AB在点A与杆OA铰接，即杆AB可绕点A转动。该系统称为双摆，其自由度数为： A.1个 B.2个 C.3个 D.4个 ” 相关考题
考题 杆OA绕固定轴0转动，长为l。某瞬时杆端A点的加速度a如图所示，则该瞬时OA 的角速度及角加速度为：
查看答案
考题 均质直角曲杆OAB的单位长度质量为ρ，OA=AB=2l，图示瞬时以角速度ω、角加速度α绕轴O转动，该瞬时此曲杆对O轴的动量矩的大小为：
查看答案
考题 均质杆OA长L，可在铅直平面内绕水平固定轴O转动。开始杆处在如图所示的稳定平衡位置。今欲使此杆转过1/4转而转到水平位置，应给予杆的另一端A点的速度vA的大小为：
查看答案
考题 在定平面Oxy 内，杆OA 可绕轴O 转动，杆AB 在点A 与杆OA 铰接，即杆AB 可绕点A 转动。该系统称为双摆，其自由度数为： （A）1 个 （B）2 个 （C）3 个 （D）4 个
查看答案
考题 T形均质杆OABC以匀角速度ω绕O轴转动，如图所示。已知OA杆的质量为2m，长为2l，BC杆质量为m，长为l，则T形杆在图示位置时动量的大小为：
查看答案
考题 均质杆OA，重P，长l，可在铅直平面内绕水平固定轴O转动。杆在图示铅直位置时静止，欲使杆转到水平位置，则至少要给杆的角速度是（　　）。
查看答案
考题 均质细直杆OA长为l，质量为m，A端固结一质量为m的小球（不计尺寸），如图所示。当OA杆以匀角速度绕O轴转动时，该系统对O轴的动量矩为：
查看答案
考题 匀质杆质量为m，长OA=l，在铅垂面内绕定轴o转动。杆质心C处连接刚度系数是较大的弹簧，弹簧另端固定。图示位置为弹簧原长，当杆由此位置逆时针方向转动时，杆上A点的速度为VA，若杆落至水平位置的角速度为零，则vA的大小应为：
查看答案
考题 均质细直杆OA长为l ，质量为m，A端固结一质置为m的小球（不计尺寸），如图所示。当OA杆以匀角速度w绕O轴转动时，该系统时O轴的动量矩为：
查看答案
考题 如图所示质量为m、长为l的均质杆OA绕O轴在铅垂平面内作定轴转动。已知某瞬时杆的角速度为ω，角加速度为α，则杆惯性力系合力的大小为（　　）。
查看答案
考题 杆OA绕固定轴O转动，长为l，某瞬时杆端A点的加速度a如题52图所示。则该瞬时OA的角速度及角加速度为（　　）。
查看答案
考题 细直杆AB由另二细杆O1A与O2B铰接悬挂。O1ABO2并组成平等四边形。杆AB的运动形式为： A.平移（或称平动） B.绕点O1的定轴转动 C.绕点D的定轴转动(O1D)=DO2=BC=l/2,AB=l D.圆周运动
查看答案
考题 在光滑水平面上，放置一静止的匀质直杆AB，当AB上受一力偶m作用时，AB将绕( )转动。 A.A.点 B.B.点 C.C.点 D.先绕A.点转动，然后绕C.点转动
查看答案
考题 直角刚杆OAB可绕固定轴O在图示平面内转动，已知OA=40cm，AB=30cm，ω=2rad/s，α=1rad/s2，则图示瞬时，B点加速度在y方向的投影为( )。 A.40C.m/s2 B.200C.m/s2 C.-200C.m/s2 D.50C.m/s2
查看答案
考题 杆OA绕固定轴O转动，长为l。某瞬时杆端A点的加速度a如图所示，则该瞬时OA的角速度及角加速度为（　　）。
查看答案
考题 在图示定平面Oxy内，杆OA可绕轴O转动，杆AB在点A与杆OA铰接，即杆AB可绕点A转动。该系统称为双摆，其自由度数为： A.1个 B.2个 C.3个 D.4个
查看答案
考题 均质细直杆OA的质量为m，长为l，以匀角速度W绕O轴转动如图所示，此时将OA杆的惯性力系向O点简化。其惯性力主矢和惯性力主矩的数值分别为（　　）。
查看答案
考题 杆OA=l，绕固定轴O转动，某瞬时杆端A点的加速度a如图所示，则该瞬时杆OA的角速度及角加速度分别为：
查看答案
考题 曲柄OA在如图30-9所示瞬时以ω的角速度绕轴O转动，并带动直角曲杆O1BC在如图所示平面内运动。若取套筒A为动点，杆O1BC为动系，则牵连速度大小为（　　）。
查看答案
考题 杆OA = l，绕固定轴O转动，某瞬时杆端A点的加速度a如图所示，则该瞬时杆OA的角速度及角加速度为：
查看答案
考题 直角刚杆OAB可绕固定轴O在图示平面内转动，己知OA= 40cm, AB= 30cm, ω=2rad/s, α= 1rad/s2,则图4-43所示瞬时，B点加速度在y方向的投影为（ ）cm/s2。 A. 40 B. 200 C. 50 D. -200
查看答案
考题 曲柄机构在其连杆AB的中点C与CD杆铰接，而CD杆又与DF杆铰接，DE杆可绕E点转动。曲柄OA以角速度ω= 8rad/s绕O点逆时针向转动。且OA = 25cm，DE=100cm。在图示瞬时，O、A、B三点共在一水平线上，B、E两点在同一铅直线上，∠CDE=90°，则此时DE杆角速度ωDE的大小和方向为：
查看答案
考题 图示质量为m、长为l的杆OA以的角速度绕轴O转动，则其动量为：
查看答案
考题 杆OA=l,绕固定轴O转动，某瞬时杆端A点的加速度a如图4-41所示，则该瞬时杆OA的角速度及角加速度为（ ）。
查看答案
热门标签
最新试卷