网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
半径为R的均匀带电球面，若其而电荷密度为σ，则在球而外距离球而R处的电场强度大小为（ ）。


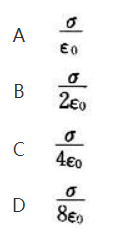
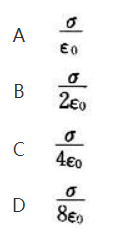
参考答案

参考解析
解析：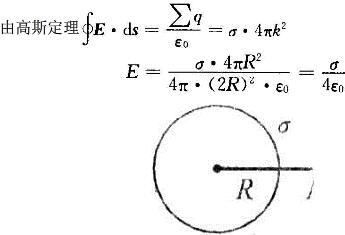
更多 “半径为R的均匀带电球面，若其而电荷密度为σ，则在球而外距离球而R处的电场强度大小为（ ）。 ” 相关考题
考题 一半径为R的均匀带电球壳,在其球心O处放置一点电荷q,该电荷受的电场力为零,若该电荷偏离球心O,则该电荷q的受力情况为()。 A、变大B、变小C、不变D、无法判断
查看答案
考题 如图，半径为a，电荷线密度ρL（r）为常数的均匀带电圆环在轴线上的电场强度为（　　）。
查看答案
考题 在真空中，半径为R的均匀带电半球面，其面电荷密度为σ，该半球面球心处的电场强度值为（　　）。
查看答案
考题 在真空中，有一半径为R的均匀带电球面，面密度为σ，球心处的电场强度为（　　）。
查看答案
考题 无限大真空中一半径为a的球，内部均匀分布有体电荷，电荷总量为q。在r a的球外 任一点r处的电场强度的大小E为（）V/m。
查看答案
考题 空气中半径为R的球域内存在电荷体密度ρ＝0.5r的电荷，则空间最大的电场强度值为（　　）。 A． R2/（8ε0） B． R/（8ε0） C． R2/（4ε0） D． R/（4ε0）
查看答案
考题 在真空中，电荷体密度为P的电荷均匀分布在半径为a的整个球体积中，则在球体中心处的电场强度E为（　　）。（设球内的介电常数为εο）
查看答案
考题 无线大真空中有一半径为a的球，内部均匀分布有体电荷，电荷总量为q，在r＜a的球内部，任意－r处电场强度的大小 为（　　）V/m。 A． qr/（4πε0a） B． qr/（4πε0a2） C． q/（4πε0r2） D． qr/（4πε0a3）
查看答案
考题 无限大真空中一半径为a的带电导体球，所带体电荷在球内均匀分布，体电荷总量为q。在球外(即r a处)任一点r处的电场强度的大小E为（ ）V/m。
查看答案
考题 真空中有一均匀带电球表面，半径为R，电荷总量为q，则球心处的电场强度大小应为下列哪项数值？（　　）
查看答案
考题 一半径为R的半球面，均匀地分布着电荷面密度为盯的电荷，则球心处的电场强度是多少
查看答案
考题 如图所示，一个均匀带电，内、外半径分别为R1和R2的均匀带电球壳，所带电荷体密度为P，A点的电势是（　　）。
查看答案
考题 半径为R的均匀带电球面，若其电荷面密度为σ，则在距离球面R处的电场强度大小为( )。 A． B． C． D．
查看答案
考题 在半径为R的球体内，电荷分布是球对称的，电荷体密度为ρ = ar(0≤r≤R)，ρ= 0(r＞R),其中α为大于O的常数，在球体内部，距球心为；x处的电场强度为( )。
查看答案
考题 半径为R的“无限长”均匀带电圆柱而的静电场中各点的电场强度的大小E与距离r的关系曲线为。（ ）
查看答案
考题 电真空中无限长、半径为a的带电圆筒上电荷面密度为σ（σ是常数），则圆筒内与轴线相距r处的电场强度为（）。A、0B、aσ／ε0r）erC、C.rσ／4πε0erD、∞
查看答案
考题 一金属球壳的内、外半径分别为R1和R2，带电荷为Q，在球心处有一电荷为q的点电荷，则球壳内表面上的电荷面密度ρ=（）
查看答案
考题 半径为R的均匀带电球面，若其电荷面密度为σ，周围空间介质的介电常数为ε0，则在距离球心R处的电场强度为（）A、σ/ε0B、σ/2ε0C、σ/4ε0D、σ/8ε0
查看答案
考题 带电量Q的导体A置于外半径为R的导体球壳B内，则球壳外离球心r处的电场强度大小（），球壳的电势（）。
查看答案
考题 半径为R1、R2的同心球面上，分别均匀带电q1和q2，其中R2为外球面半径，q2为外球面所带电荷量，设两球面的电势差为ΔU，则（）A、ΔU随q1的增加而增加B、ΔU随q2的增加而增加C、ΔU不随q1的增减而改变D、ΔU不随q2的增减而改变
查看答案
考题 半径为R的不均匀带电球体，电荷体密度分布为ρ=Ar，式中r为离球心的距离（r≤R），A为一常数，则球体中的总电量（）
查看答案
考题 均匀带电球面，球面半径为R，总带电量为q，则球心O处的电场E0=（），球面外距球心r处一点的电场Eφ=（）。
查看答案
考题 均匀带电球面，电荷面密度为σ，半径为R，球面内任一点的电势为（）。A、不能确定B、与球心处相同C、与球心处不同D、为零
查看答案
考题 一半径为R的导体球表面的面点荷密度为σ，则在距球面R处的电场强度（）。A、σ/ε0B、σ/2ε0C、σ/4ε0D、σ/8ε0
查看答案
考题 两个半径分别为21RR和的同心均匀带电球面，且R2=2R1内球面带电量q1〉0，外球带电量q2满足（）条件时能使内球的电势为正：满足（）条件时能使内球的电势为零；满足（）条件时，能使内球的电势为负。
查看答案
考题 均匀带电圆环带电量q，圆环半径为R，则圆环中心点处的电场强度大小为（）。
查看答案
考题 单选题半径为R的均匀带电球面，若其电荷面密度为σ，则在距离球面R处的电场强度大小为( )。A σ/ε0B σ/2ε0C σ/4ε0D σ/8ε0
查看答案
热门标签
最新试卷