2022年结构工程师《基础考试(一级)》章节练习(2022-01-20)
发布时间:2022-01-20
2022年结构工程师《基础考试(一级)》考试共题,分为。小编为您整理第二章 普通物理5道练习题,附答案解析,供您备考练习。
1、压强为p、体积为V的水蒸气( 视为刚性分子理想气体)的内能为( )。【单选题】
A.7pV/2
B.5pV/2
C. pV/2
D.3pV
正确答案:D
答案解析:水蒸气分子运动的自由度数i=6,由理想气体状态方程pV= (m/M) ·RT和内能公式E=(i/2)·(m/M)·RT,联立可得E=ipV/2=3pV。
2、已知平面简谐波的方程为y=Acos (Bt-Cx),式中A、B、C为正常数,此波的波长和波速分别为( )。【单选题】
A.B/C,2π/C
B.2r/C,B/C
C.π/C,2B/C
D.2π/C,C/B
正确答案:B
答案解析:将方程y=Acos (Bt-Cx)与平面简谐波的标准方程y= Acosω (t-x/u)对比得:波速u=B/C,ω=B。又由于ω=2π/T, u=λT,得波长: λ=2π/C。
3、一平面简谐波沿x轴正向传播,振幅A=0.02m,周期T=0.5s,波长λ= 100m,原点处质元初相位φ=0,则波动方程的表达式( )。【单选题】
A.y=0.02cos2π (t/2-0.01x) (SI)
B.y=0.02cos2π (2t-0.01x) (SI)
C.y=0.02cos2π (t/2-100x) (SI)
D.y=0.002cos2π (2t-100x) (SI)
正确答案:B
答案解析:沿x轴正向传播的波动方程表达式为: 又u=λT,∞=2π/T,故波动方程写为: 由于A=0.02m,T=0.5s,λ= 100m,代入波动方程公式可得:y=0.02cos2π (2t-0.01x) (SI)。
4、在双缝干涉实验中,光的波长600nm,双缝间距2mm,双缝与屏的间距为300cm,则屏上形成的干涉图样的相邻明条纹间距为( )。【单选题】
A.0.45mm
B.0.9mm
C.9mm
D.4.5mm
正确答案:B
答案解析:相邻明(或暗)纹的间距为:Δx=Dλd。 式中,D为双缝与屏的间距;d为双缝间距; n为波长。代入数据得:Δx=Dλ/d= (3000/2) ×600×10 fmm=0.9mm。
5、两相干波源,频率为100Hz,相位差为π,两者相距20m,若两波源发出的简谐波的振幅均为A,则在两波源连线的中垂线上各点合振动的振幅为( )。【单选题】
A.-A
B.0
C.A
D.2A
正确答案:B
答案解析:当两相千波源发出的波在某一点的相位差的整数倍时,合振动的振幅当为π的奇数倍时,合振动的振幅在波源连线的中垂线上,相位故合振幅
下面小编为大家准备了 结构工程师 的相关考题,供大家学习参考。


若该过梁承受弯矩设计值M=6.5kN·m,采用钢筋砖过梁,则在砖过梁底部的钢筋配置面积最接近于( )mm2。(钢筋采用HPB235)
B..55.2
C..61.7
D..65.2


题28:假定,首层一字形独立墙肢W1考虑地震组合且未按有关规定调整的一组不利内力计算值Mw=15000kN·m,Vw=2300kN,剪力墙截面有效高度hw0=4200mm,混凝土强度等级C35。试问,满足规范剪力墙截面名义剪应力限值的最小墙肢厚度b(mm),与下列何项数值最为接近?( )
提示:按《高层建筑混凝土结构技术规程》(JGJ 3—2010)作答。
B. 300
C. 350
D. 400
根据《高规》第7.2.7条,剪力墙剪跨比为:λ=M^c/(Vchw0)=15000×10^6/(2300×10^3×4200)=1.55<2.5。剪跨比小于2.5时,根据《高规》式(7.2.7-3)剪力墙墙肢截面剪力设计值应按下式计算:Vw≤(0.15βcfcbwhw0)/γRE,代入数据即:3680≤(0.15×1.0×16.7×bw×4200)×10^-3/0.85;解得:bw≥297.3mm。
最小墙肢厚度与300mm最为接近,故答案选B。
【考点分析】
本题主要考查以下内容:
①对剪力墙“强剪弱弯”的理解;
②不同剪跨比的剪力墙名义剪应力的控制要求。
【解题思路】
本题解题分析步骤如下:
①根据规范确定剪力增大系数;
②计算剪跨比;
③本题墙肢剪跨比小于2.5,按《高规》式(7.2.7-3)代入相关数值可得墙肢最小厚度要求。
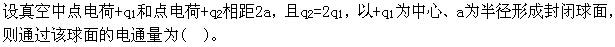
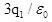
B.
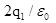
C.
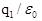
D.0

B.运算器
C.存储器
D.I/D.接口
声明:本文内容由互联网用户自发贡献自行上传,本网站不拥有所有权,未作人工编辑处理,也不承担相关法律责任。如果您发现有涉嫌版权的内容,欢迎发送邮件至:contact@51tk.com 进行举报,并提供相关证据,工作人员会在5个工作日内联系你,一经查实,本站将立刻删除涉嫌侵权内容。
- 2021-10-02
- 2021-11-24
- 2021-11-18
- 2021-01-03
- 2020-05-16
- 2021-08-15
- 2021-12-03
- 2021-01-05
- 2020-12-07
- 2020-05-26
- 2020-06-17
- 2021-04-25
- 2020-12-19
- 2020-04-10
- 2021-10-27
- 2020-07-15
- 2021-10-19
- 2021-07-28
- 2021-08-01
- 2021-11-30
- 2021-05-27
- 2020-10-09
- 2021-11-11
- 2020-08-10
- 2021-07-13
- 2021-11-18
- 2021-12-01
- 2020-05-06
- 2020-04-28
- 2021-09-10