2021年环保工程师《基础知识》历年真题(2021-01-25)
发布时间:2021-01-25
2021年环保工程师《基础知识》考试共题,分为。小编为您整理历年真题10道,附答案解析,供您考前自测提升!
1、四连杆机构如图所示,已知曲柄且角速度为w,角加速度为α,则杆AB的中点M的速度、法向和切向加速度的大小分別为:【单选题】
A.
B.
C.
D.
正确答案:C
答案解析:因为点A、B两点的速度、加速度方向相同,大小相等.根据刚体做平行移动时的特性,可判断杆AB的运动形式为平行移动,因此,平行移动刚体上M点和A点有相 同的速度和加速度,即:
2、对于图示电路,可以列写a、b、c、d4个结点的KCL方程和①、②、③、④、⑤5个回路的KVL方程。为求出6个未知电流正确的求解模型应该是:【单选题】
A.任选3个KCL方程和3个KVL方程
B.任选3个KCL方程和①、②、③3个回路的KVL方程
C.任选3个KCL方程和①、②、④3个回路的KVL方程
D.写出4个KCL方程和任意2个KVL方程
正确答案:B
答案解析:该电路具有6条支路,为求出6个独立的支路电流,所列方程数应该与支路 数相等,即要列出6阶方程。正确的列写方法是:KCL独立节点方程=节点数一1 = 4-1 = 3KVL独立回路方程(网孔数)=支路数一独立节点数=6 — 3 = 3“网孔”为内部不含支路的回路。
3、函数f(x,y)在点处的一阶偏导数存在是该函数在此点可微分的:【单选题】
A.必要条件
B.充分条件
C.充分必要条件
D.既非充分条件也非必要条件
正确答案:A
答案解析:本题考查多元函数微分学的概念性问题,涉及多元函数偏导数与多元函数连 续等概念,需记忆下图的关系式方可快速解答: 可知,函数可微不能推出一阶偏导数存在,而函数一阶偏导数存在可以推出函数可 微,故而是必要条件。
4、设函数z= 其中f(x)具有二阶导数,则等于:【单选题】
A.
B.
C.
D.
正确答案:D
答案解析:本题考查多元函数的混合偏导数求解。
5、—平面简谐波的波动方程为y = 0. 02cosπ(50t + 4x)(SI),此波的振幅和周期分别为:【单选题】
A.0. 02m,0, 04s
B.0. 02m.0. 02s
C.-0. 02m,0. 02s
D.0. 02m,25s
正确答案:A
答案解析:
6、函数f(x)=(a〉0,a≠1)的麦克劳林展开式中的前三项是:【单选题】
A.
B.
C.
D.
正确答案:C
答案解析:本题考查麦克劳林展开式的基本概念。麦克劳林展开式的一般形式为
7、在图示结构中,已知AB = AC=2r,物重其余质量不计,则支座A的约束力为:【单选题】
A.
B.
C.
D.
正确答案:D
答案解析:取整体为研究对象,受力如解图所示。
8、下列级数中,发散的是:【单选题】
A.
B.
C.
D.
正确答案:C
答案解析:本题考查级数中常数项级数的敛散性。判断此类问题应注意和调和级数比较,以及级数的相关性质。
9、有一变截面压力管道,测得流量为15L/s,其中一截面的直径为100mm,另一截 面处的流速为20m/s.则此截面的直径为:【单选题】
A.29mm
B.31mm
C.35mm
D. 26mm
正确答案:B
答案解析:
10、实心圆轴受扭,若将轴的直径减小一半,则扭转角是原来的:【单选题】
A.2倍
B. 4倍
C.8倍
D.16倍
正确答案:D
答案解析:设实心圆轴直径为d,则:
下面小编为大家准备了 环保工程师 的相关考题,供大家学习参考。
B.第一级明纹
C.第二级暗纹
D.第二级明纹

当a缩小一半,k=3的暗纹变为k=1的明纹。
B、碘晶体
C、SiO2晶体
D、TiO2晶体
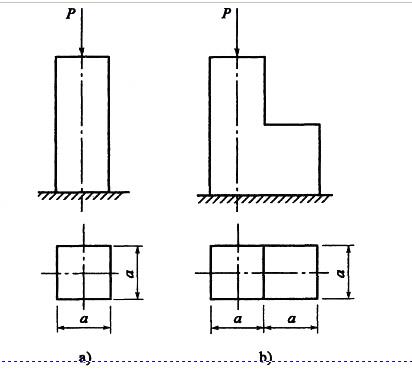
B.提高不到一倍
C.不变
D.降低
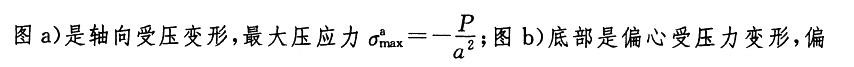
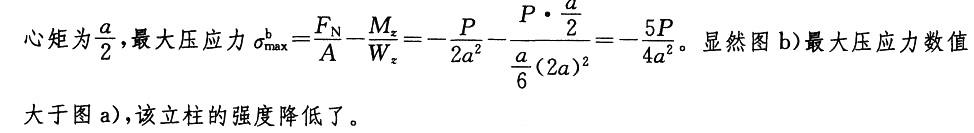
声明:本文内容由互联网用户自发贡献自行上传,本网站不拥有所有权,未作人工编辑处理,也不承担相关法律责任。如果您发现有涉嫌版权的内容,欢迎发送邮件至:contact@51tk.com 进行举报,并提供相关证据,工作人员会在5个工作日内联系你,一经查实,本站将立刻删除涉嫌侵权内容。
- 2020-06-04
- 2020-06-21
- 2020-05-11
- 2020-08-30
- 2020-10-14
- 2020-05-22
- 2020-08-31
- 2021-08-23
- 2021-02-13
- 2021-04-08
- 2021-02-11
- 2020-10-14
- 2020-08-20
- 2020-11-14
- 2020-06-23
- 2021-04-03
- 2020-06-25
- 2021-09-12
- 2020-06-01
- 2020-08-08
- 2021-08-04
- 2021-04-17
- 2020-08-04
- 2020-08-23
- 2020-06-09
- 2021-06-11
- 2020-06-03
- 2020-12-12
- 2020-10-28
- 2021-02-21