网友您好, 请在下方输入框内输入要搜索的题目:
文中( 5 )处正确的答案是( )。
A.单调递增函数
B.单调递减函数
C.对数函数
D.指数函数
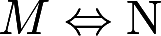 表示“M的充分必要条件是N”,则必有
表示“M的充分必要条件是N”,则必有
AF(x)是偶函数
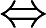 f(x)是奇函数
f(x)是奇函数
BF(x)是奇函数
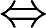 f(x)是偶函数
f(x)是偶函数
CF(x)是周期函数
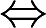 f(x)是周期函数
f(x)是周期函数
DF(x)是单调函数
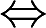 f(x)是单调函数
f(x)是单调函数
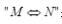
表示“M的充分必要条件是N”,则必有( )。
B.F(x)是奇函数f(x)是偶函数
C.F(x)是周期函数f(x)是周期函数
D.F(x)是单调函数f(x)是单调函数

B.单调递减且曲线为凸的
C.单调递增且曲线为凸的
D.单调递减且曲线为凹的
B.单调递减且曲线为凸的
C.单调递增且曲线为凸的
D.单调递减且曲线为凹的
广东省11大市2013届高三数学(理)一模试题分类汇编三角函数一、选择、填空题1、(广州市2013届高三3月毕业班综合测试试题(一)函数是A奇函数且在上单调递增 B奇函数且在上单调递增 C偶函数且在上单调递增 D偶函数且在上单调递增 答案:C2、(江门市2013届高三2月高考模拟)在中,若,则A B C D答案:D3、(揭阳市2013届高三3月第一次高考模拟)当时,函数取得最小值,则函数 A是奇函数且图像关于点对称 B是偶函数且图像关于点对称 C是奇函数且图像关于直线对称 D是偶函数且图像关于直线对称答案:C4、(梅州市2013届高三3月总复习质检)函数图象上各点的横坐标缩短到原来的倍(纵坐标不变),右平移个单位,那么所得图象的一条对称轴方程为A、B、C、D、答案:B5、(汕头市2013届高三3月教学质量测评)把函数y=cos2xl的图像上所有点的横坐标伸长到原来的2倍纵坐标不变),然后向左平移l个单位长度再向下平移1个单位长度得到的图像是 答案:A6、(韶关市2013届高三调研考试)ABC中,角A,B,C所对边a,b,c,若a3,C120,ABC的面积S,则c()A、5B、6C、D、7答案:D7、(深圳市2013届高三2月第一次调研考试)化简的结果是A B C D答案:C8、(肇庆市2013届高三3月第一次模拟考试)在中, ,BC=2,则的面积等于_.答案:9、(佛山市2013届高三教学质量检测(一)函数 的最小正周期为 ,最大值是 答案:(2分), (3分)10、(茂名市2013届高三第一次高考模拟考试)已知函数,则下列结论正确的是( )A. 此函数的图象关于直线对称 B. 此函数的最大值为1C. 此函数在区间上是增函数 D. 此函数的最小正周期为 答案:C11、(湛江市2013届高三高考测试(一)在ABC中,A,AB2,且ABC的面积为,则边AC的长为A、1B、C、2D、1答案:A二、解答题1、(广州市2013届高三3月毕业班综合测试试题(一)已知函数(其中,)的最大值为2,最小正周期为.(1)求函数的解析式;(2)若函数图象上的两点的横坐标依次为,为坐标原点,求 的面积.(1)解:的最大值为2,且, . 1分的最小正周期为, ,得. 2分. 3分(2)解法1:, 4分, 5分. 8分.10分. 11分的面积为.12分解法2:, 4分, 5分. . 8分. 10分. 11分的面积为.12分解法3:, 4分, 5分.直线的方程为,即. 7分点到直线的距离为. 9分, 11分的面积为. 12分2、(江门市2013届高三2月高考模拟)已知函数(,)的最小值为求;若函数的图象向左平移()个单位长度,得到的曲线关于轴对称,求的最小值解:因为函数(,)的最小值为,所以,2分,4分函数的图象向左平移()个单位长度,得6分因为的图像关于轴对称,所以8分解得10分因为,所以的最小值为12分3、(揭阳市2013届高三3月第一次高考模拟)在中,角所对的边分别为,且满足(1)求角的大小;(2)求的最大值,并求取得最大值时角的大小解:(1)由结合正弦定理得,-2分从而,-4分,;-6分(2)由(1)知-7分-8分 -9分 -10分,当时,取得最大值,-11分此时-12分4、(梅州市2013届高三3月总复习质检)已知ABC的内角A,B,C的对边分别为a,b,c,满足。(1)求角C(2)若向量与共线,且c3,求a、b的值。5、(汕头市2013届高三3月教学质量测评)ABC中内角A,B,C的对边分别为a,b,c, 向量,且。 (I)求角A的大小;(II)若且ABC的面积为,求b十c的值。解:(1) (2分) (4分) 又 (6分) (2) (8分) (9分) 由余弦定理得:(10分) (11分) (12分)6、(韶关市2013届高三调研考试)函数的部分图象如右所示。(1)求函数f(x)的解析式(2)设,且,求的值。解:(1)由图可知T,所以,2,A2所以(2),即,又,所以,所以7、(深圳市2013届高三2月第一次调研考试)已知函数,点、分别是函数图像上的最高点和最低点(1)求点、的坐标以及的值;(2)设点、分别在角、的终边上,求的值【解析】(1), , 当,即时,取得最大值; 当,即时,取得最小值 因此,点、的坐标分别是、 (2)点、分别在角、的终边上, , 【说明】 本小题主要考查了三角函数的图象与性质,三角恒等变换,以及平面向量的数量积等基础知识,考查了简单的数学运算能力8、(肇庆市2013届高三3月第一次模拟考试)已知函数在时取得最大值2.(1)求的最小正周期;(2)求的解析式;(3)若,求的值.解:(1)的最小正周期为 (2分)(2)由的最大值是2知, (3分)又,即, (4分), (5分) (6分)(3)由(2)得,即,
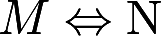 表示“M的充分必要条件是N”,则必有
表示“M的充分必要条件是N”,则必有
AF(x)是偶函数
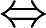 f(x)是奇函数
f(x)是奇函数
BF(x)是奇函数
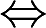 f(x)是偶函数
f(x)是偶函数
CF(x)是周期函数
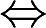 f(x)是周期函数
f(x)是周期函数
DF(x)是单调函数
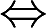 f(x)是单调函数
f(x)是单调函数
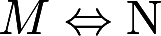 表示“M的充分必要条件是N”,则必有
表示“M的充分必要条件是N”,则必有
AF(x)是偶函数
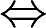 f(x)是奇函数
f(x)是奇函数
BF(x)是奇函数
 f(x)是偶函数
f(x)是偶函数
CF(x)是周期函数
 f(x)是周期函数
f(x)是周期函数
DF(x)是单调函数
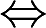 f(x)是单调函数
f(x)是单调函数
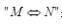
表示“M的充分必要条件是N”,则必有( )。
B.F(x)是奇函数f(x)是偶函数
C.F(x)是周期函数f(x)是周期函数
D.F(x)是单调函数f(x)是单调函数

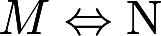 表示“M的充分必要条件是N”,则必有
表示“M的充分必要条件是N”,则必有
AF(x)是偶函数
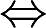 f(x)是奇函数
f(x)是奇函数
BF(x)是奇函数
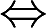 f(x)是偶函数
f(x)是偶函数
CF(x)是周期函数
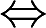 f(x)是周期函数
f(x)是周期函数
DF(x)是单调函数
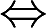 f(x)是单调函数
f(x)是单调函数
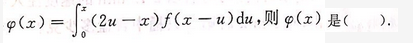
B.单调减少的偶函数
C.单调增加的偶函数
D.单调减少的偶函数

更多 “广东省11大市2013届高三数学一模试题分类汇编9 三角函数 理” 相关考题
- 慢性化脓性中耳炎可分为下列哪几型()A、单纯型B、颅内型C、骨疡型D、胆脂瘤型E、溃疡型
- 在国际避税地中,属于征收正常税收,但提供某些特殊的税收优惠的国家是() A、加拿大B、巴哈马C、中国D、以色列
- 危机干预的最高目标是()A、确定需要紧急处理的问题B、帮助当事人制定一个明确而切实可行的目标及特别的行动和时间表C、帮助当事人获得新的应付技能,促进症状的明显改善D、帮助当事人度过危机,恢复心理健康并实现促进成长E、向当事人提供必要的保证和支持
- 牙槽嵴修整术适宜时间应在拔牙后()A、2~3周B、4~5周C、6~7周D、7~8周E、8~12周
- 癫痫的年发病率为()A、50%~70%B、50‰~70‰C、50/万~70/万D、50/10万~70/10万E、50/100万~70/100万
- 某患者,女,55岁,1年来右眶上缘、鼻翼旁因触摸多次发生刀割样剧痛,每次最长持续约2-3分钟。则该患者诊断可能为()A、三叉神经第一支痛B、三叉神经第二支痛C、三叉神经第三支痛D、三叉神经第一、二支痛E、三叉神经第二、三支痛
- 抑郁发作的病程标准为至少()A、1周B、2周C、3周D、10天E、4周
- 女患,78岁,5年前逐渐出现记忆力减退,逐渐加重,出门经常找不到家,近2年来生活渐渐不能自理,神经系统检查未见局灶性神经系统体征,MMSE评分8分,头颅MRI显示脑萎缩,实验室检查未见异常。根据NINCDS-ADR-DA的国际标准,该患的诊断为()A、确定的Alzheimer病B、可能的Alzheimer病C、血管性痴呆D、可能性大的Alzheimer病E、路易体痴呆
- 甲国A公司某年获利20万元,收到在乙国的子公司的股息3.5万元,甲国的税率为40%。子公司同年获利10万元。在乙国规定的30%的税率基础上,享受减半征收1.5万元所得税的优惠实际向乙国缴纳所得税1.5万元。试计算在税收饶让条件下,甲国应向A公司征收的所得税税额。
- 患者男性,62岁,发现高血压12年,近4年出现胸骨后疼痛,诊断为原发性高血压、冠心病(心绞痛型),给予硝苯地平和β受体阻滞剂口服。1天前突然出现气急、咳嗽、咳泡沫样痰。检查:端坐呼吸,血压150/90mmHg,心率130次/分,房颤心律,双肺底可闻及湿啰音,下肢无水肿。此患者出现病情加重的可能诱因是()A、呼吸道感染B、肾功能不全C、钠摄入过多D、精神紧张E、药物负性肌力作用