全等三角形难题(含答案解析)

网友您好，请在下方输入框内输入要搜索的题目：

全等三角形难题(含答案解析)

△ABC中，AB=13cm，BC=10cm，BC边上的中线AD=12cm.求AC

对边相等,对角相等的凸四边形,是平行四边形吧?

方法①∠B小于90°；

左上为A，左下为B，右下为C，右上为D；

已知∠B=∠D；AB=CD;

证明：过A作AN⊥BC于N；

过C作CM⊥AD于M；

连接AC

∵AN⊥BC；CM⊥AD

∴∠ANB=∠DMC=90°

又∵∠B=∠D；AB=CD

∴△ANB=△DMC(AAS）

∴AN=CM;BN=DM

又∵∠ANB=∠DMC=90°，AC=AC

∴△ACD=△AMD（HL）

∴AM=DN

又∵BN=DM

∴BD=AC

∵BD=AC；AB=CD

∴凸四边形ABCD为平行四边型。

方法②∠B大于90°

左上为A，左下为B，右下为C，右上为D；

已知∠B=∠D；AB=CD;

证明：延长CD,过A作AN⊥BC于N；

延长AB,过C作CM⊥AD于M；

连接AC

∵AN⊥BC；CM⊥AD

∴∠ANB=∠DMC=90°

又∵∠B=∠D；AB=CD

∴△ANB=△DMC(AAS）

∴AN=CM;BN=DM

又∵∠ANB=∠DMC=90°，AC=AC

∴△ACD=△AMD（HL）

∴AM=DN

又∵BN=DM

∴BD=AC

∵BD=AC；AB=CD

∴凸四边形ABCD为平行四边型。

方法③∠B等于90°

证明：∵∠B=∠D=90°；AB=CD；AC=AC

∴△ABC=△ADC（HL）

∴AB=CB

∵BD=AC；AB=CD

∴凸四边形ABCD为平行四边型。

有错吗？若我的证明有错请明示，我知道有个反例，但它是凹四边形。

是平行四边形

如图．已知圆⊙O是△ABC的外接圆，AD是圆⊙0的直径，且BD=BC，延长AD到E，且有∠EBD=∠CAB。

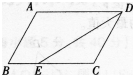
(1)求证：BE是⊙0的切线；
(2)若BC=√3，AC=5，求圆的直径AD及切线BE的长。

答案：

解析：

(1)连接OB，∵AD是圆⊙O的直径'∴∠OBD+∠EBD=90°， ∵BD=BC,∴其劣弧所对的圆周角相等，即∠CAB=∠BAD，
∵AO=BO,∴∠BAD=∠ABO，
又∠EBD=∠CAB,∴∠EBD=ABO,∴∠OBD+∠ABO=90°,∴∠OBE=90°，
∵B0是圆的半径，∴BE是⊙O的切线。
(2)设圆的半径为r，连接CD交OB于F，

设圆的半径为R，连接CD，.

如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2.

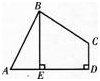
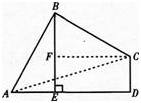
(1)求证：AB=BC；
(2)当BE⊥AD于E时，试证明：BE=AE+CD.

答案：

解析：

如图，平行四边形ABCD，∠ADC的角平分线DE交BC于E,且AD=14，DC=9，则BE/EC的值为()。

A.1/3
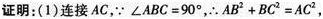
B.4/9
C.5/9
D.2/3

答案：C

解析：

AD∥BC，则∠ADE=∠DEC，又∠ADE=∠CDE，所以△CDE为等腰三角形，EC=CD=9，

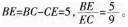
摘要:全等三角形难题(含答案)1.已知：AB=4，AC=2，D是BC中点，AD是整数，求ADABCD解：延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=22.已知：D是AB中点，∠ACB=90°，求证：CDADCB延长CD与P，使D为CP中点。连接AP,BP∵DP=DC,DA=DB∴ACBP为平行四边形又∠ACB=90∴平行四边形ACBP为矩形1AB2∴AB=CP=1/2AB3.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2A12EBCFD证明：连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。∵∠ABC=∠AED。∴∠ABE=∠AEB。∴AB=AE。在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。∴∠BAF=∠EAF(∠1=∠2)。4.已知：∠1=∠2，CD=DE，EF//AB，求证：EF=ACA12FCDEB过C作CG∥EF交AD的延长线于点GCG∥EF，可得，∠EFD＝CGDDE＝DC∠FDE＝∠GDC（对顶角）∴△EFD≌△CGDEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=

如下图所示，A、B、C、D为一块梯形田地的4个顶点。已知BC比AD长16米，三角形ACD面积比ABC小200平方米。问AD到BC的距离是多少米？

A.12.5
B.18.5
C.20
D.25

答案：D

解析：

第一步，本题考查几何问题，属于平面几何类。
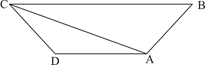
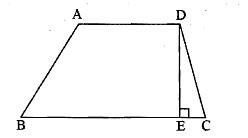
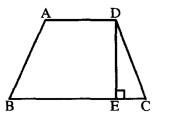
第二步，设AD为x,AD距离BC为h，根据题意得

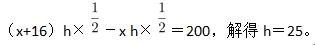
如图所示，梯形ABCD，AD∥BC，DE⊥BC，现在假设AD、BC的长度都减少10%，DE的长度增加10%，则新梯形的面积与原梯形的面积相比，会怎样变化？

A. 不变
B. 减少1%
C. 增加10%
D. 减少10%

答案：B

解析：

解题指导： S=90％（AD+BC）*100％DE÷2=99（AD+BC）*DE÷2，所以减少了1％。故答案为B。

如下图所示，A、B、C、D为一块梯形田地的4个顶点。已知BC比AD长16米，三角形ACD面积比ABC小200平方米。问AD到BC的距离是多少米？

A.12.5
B.18.5
C.20
D.25

答案：D

解析：

第一步，本题考查几何问题，属于平面几何类。
第二步，设AD为x,AD距离BC为h，根据题意得

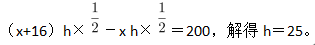
如图所示，梯形ABCD，AD//BC,DE丄BC,现在假设AD、BC的长度 ’都减少10%，DE的长度增加10%，则新梯形的面积与原梯形的面积相比，会（）。

A.不变 B.减少1% B-ECC.增加10% D.减少10%

答案：B

解析：

梯形 ABCD 的面积= (AD+BC)XDE/2;AD、BC的长度都减少10%,DE的长度增加10%,则梯形ABCD的面积=(1 一 10%) X (AD+BC) X (1 +10 %) X DE/2 = 99 % X ( AD+BC) X DE/2。新梯形的面积与原梯形的面积相比，减少1%。

给定关系模式R小于U，F大于，其中U=｛ABCDE｝，F={AB→DE，AC→E，AD→B，B→C,C→D｝，则R的所有候选码为（请作答此空）,关系R属于（）。

A. AB、AC
B. AB、AD
C. AC、AD
D. AB、AC、AD

答案：D

解析：

本题考查关系理论的基础知识。根据候选码求解算法，求解该关系模式的码：①必然出现在候选码中的属性为A；不出现在候选码中的属性为E；待考察的属性为BCD；②(A)+=A，不包含全部属性，不是候选码；③(AB)+=ABDEC包含全部属性，是候选码；(AC)+=ACEDB包含全部属性，是候选码；(AD)+=ADBCE包含全部属性，是候选码。故R的候选码为{AB、AC、AD}。

网友您好， 请在下方输入框内输入要搜索的题目：

更多 “全等三角形难题(含答案解析)” 相关考题

网友您好，请在下方输入框内输入要搜索的题目：