网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
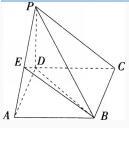
(10分)如图,四棱锥P-ABCD的底面为正方形,侧棱PD⊥底面ABCD,点E为棱PA的中点,PD=AD=1。
(1)求证:PC∥平面BDE:
(2)求三棱锥B-PDE的体积。
(1)求证:PC∥平面BDE:
(2)求三棱锥B-PDE的体积。

参考答案
参考解析
解析:(1)如图所示,连接AC,AC与BD交于点M,连接EM。因为底面ABCD是正方形,所以M为AC中点,又因为E为PA中点,所以




更多 “(10分)如图,四棱锥P-ABCD的底面为正方形,侧棱PD⊥底面ABCD,点E为棱PA的中点,PD=AD=1。 (1)求证:PC∥平面BDE: (2)求三棱锥B-PDE的体积。 ” 相关考题
考题
如图,正四面体P-ABC的棱长为a,D、E、F分别为棱PA、PB、PC的中点,G、H、M分别为DE、EF、FD的中点,则三角形GHM的面积与正四面体P-ABC的表面积之比为:
A.1:8
B.1:16
C.1:32
D.1:64
考题
连接正四面体侧棱的中点和底面的中心A、E、F、G、H构成多面体
(如右图所示)。问该多面体与正四面体的体积比是多少?( )
A. 1 : 8
B. 1 : 6
C. 1:4
D. 1 : 2
考题
如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。
(I)证明:EF∥面PAD。
(II)求三棱锥B-PFC的体积。
考题
已知四棱锥P-ABCD底面为直角梯形,AB平行于DC,∠DAB=90°,PA垂直于底面ABCD,PA=AD=DC=
AB=1,M为PB中点。
(1)求证:面PAD⊥面PCD;
(2)求面AMC与面BMC所成二面角的余弦值。
考题
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90o,E是CD的中点。
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。
考题
多选题二次对称轴出现的位置一般是()A相对棱的中点B两底面中心C一条棱与相对底面的中心D相对两柱面的中心
热门标签
最新试卷