网友您好, 请在下方输入框内输入要搜索的题目:
设(X1,X2,…,Xn)是来自正态总体N(μ,σ2)的简单随机样本,其中参数μ,σ2未知,则下列各项中,不是统计量的有( )。

解析:统计量中不含有任何未知参数,故D、E项不是统计量。

B.
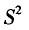
C.S
D.
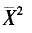

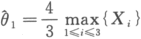 :与
:与 都是参数θ的无偏估计量,试比较其有效性.
都是参数θ的无偏估计量,试比较其有效性.

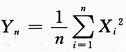 ,依概率收敛于_______.
,依概率收敛于_______.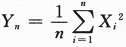 ,依概率收敛于
,依概率收敛于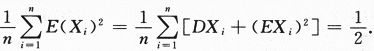 答案应填
答案应填
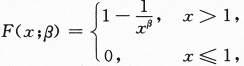
其中未知参数β>1,X1,X2,…,Xn为来自总体X的简单随机样本,求:
(Ⅰ)β的矩估计量;(Ⅱ)β的最大似然估计量.

西南大学网络与继续教育学院课程考试试题卷类别:网教 2019年6月课程名称【编号】:数理统计【0348】 A卷大作业 满分:100 分看清答题要求!一、叙述判断题(任选一题,每题15分)1、设总体X服从两点分布B(1,p),其中p是未知参数,是来自总体的简单随机样本。(1) 写出样本的联合概率分布;(2) 指出之中哪些是统计量,哪些不是统计量,为什么? 解:都是统计量,不是统计量,因p是未知参数。二、解答题(1、2任选一题,3、4、5必做)1、设总体X服从参数为(N,p)的二项分布,其中(N,p)为未知参数,为来自总体X的一个样本,求(N,p)的矩法估计。(15分)解:因为,只需以分别代解方程组得。3、为比较两个学校同一年级学生数学课程的成绩,随机地抽取学校A的9个学生,得分数的平均值为,方差为;随机地抽取学校B的15个学生,得分数的平均值为,方差为。设样本均来自正态总体且方差相等,参数均未知,两样本独立。求均值差的置信水平为0.95的置信区间。()(20分)解:根据两个正态总体均值差的区间估计的标准结论,均值差的置信水平为0.95的置信区间为4、甲、乙两台机床分别加工某种轴,轴的直径分别服从正态分布与,为比较两台机床的加工精度有无显著差异。从各自加工的轴中分别抽取若干根轴测其直径,结果如下:总体样本容量 直径X(机床甲) Y(机床乙) 8 720.5 19.8 19.7 20.4 20.1 20.0 19.0 19.920.7 19.8 19.5 20.8 20.4 19.6 20.2试问在=0.05水平上可否认为两台机床加工精度一致?()(15分)解:首先建立假设: 在n=8,m=7, =0.05时,故拒绝域为, 现由样本求得=0.2164,=0.2729,从而F=0.793,未落入拒绝域,因而在=0.05水平上可认为两台机床加工精度一致。5、某地调查了3000名失业人员,按性别文化程度分类如下:文化程度 性别大专以上 中专技校 高中 初中及以下合计男女40 138 620 104320 72 442 62518411159合计60 210 1062 16683000试在=0.05水平上检验失业人员的性别与文化程度是否有关。()(15分)解:这是列联表的独立性检验问题。在本题中r=2,c=4,在=0.05下,, 因而拒绝域为:. 为了计算统计量(3.4),可列成如下表格计算:大专以上 中专技校 高中 初中及以下男女36.8 128.9 651.7 1023.623.2 81.1 410.3 644.418411159合计60 210 1062 16683000从而得,由于=7.3267.815,样本落入接受域,从而在=0.05水平上可认为失业人员的性别与文化程度无关。三、证明题(任选一题)1、设是取自正态总体的一个样本,证明是的无偏估计、相合估计。(20分)解:由于 服从自由度为n-1的-分布,故,从而根据车贝晓夫不等式有,所以是的相合估计。- 2 -
 P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.
P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.
 服从_______分布,参数为________.
服从_______分布,参数为________.
且相互独立,故

答案应填服从F分布,参数为(10,5).
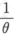 (i=1,2,…,θ,X1,X2,…,Xn为来自总体的简单随机样本,则θ的矩估计量为_______(其中θ为正整数).
(i=1,2,…,θ,X1,X2,…,Xn为来自总体的简单随机样本,则θ的矩估计量为_______(其中θ为正整数).
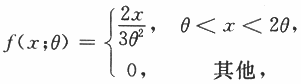 其中θ是未知参数,X1,X2,…,Xn为来自总体X的简单随机样本.若
其中θ是未知参数,X1,X2,…,Xn为来自总体X的简单随机样本.若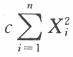 是θ的无偏估计,则c=______.
是θ的无偏估计,则c=______. 答案应填.
答案应填.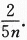

其中未知参数β>1,X1,X2,…,Xn为来自总体X的简单随机样本,求:
(Ⅰ)β的矩估计量;(Ⅱ)β的最大似然估计量.

更多 “2019年6月西南大学数理统计【0348】大作业答案” 相关考题
- 对贷款逾期期间不能按期归还的利息,按规定计收复利。
- 出票人在支票上的签章,必须与预留银行印鉴相符。
- 每一笔贷款只能展期一次.
- 固定资产、无形资产、长期待摊费用等物权形式存在的资产不属于金融资产。
- 支票的大小写金额可以更改,但更改人必须签章以明确责任。
- 中国武装力量是由人民解放军、武装警察部队和()组成。A. 基干B. 普通民兵C. 民兵D. 后备部队
- 手机依赖是种新的心理疾病吗?( )。A.不是B.不能简单判断C.不知道D.是
- “单选(5分)“我能,无限可能”和“to be NO.1”体现的是哪种需要( )A. 自我实现的需要B. 归属和爱的需要C. 生理需要D. 安全需要
- 商业银行吸收企事业单位或人人的存款是现金存款。
- ( 难度:中等)Hive适用于以下哪些应用场景A.统计上个月在网用户数B.计算近十年人均话费变化趋势C.实时计算用户套餐剩余量D.疫情期计算用户行程数据
- 浙江省Q21联盟市级名校2021-2022学年十校联考最后语文试题含解析
- 浙江省金华九中重点达标名校2021-2022学年毕业升学考试模拟卷语文卷含解析
- 上海市浦东新区第四署达标名校2021-2022学年中考冲刺卷语文试题含解析
- 深圳南山区六校联考2021-2022学年中考三模语文试题含解析
- 四川省德阳旌阳区六校联考2021-2022学年中考冲刺卷语文试题含解析
- 四川省仁寿县重点中学2022年中考适应性考试语文试题含解析
- 唐山市林西中学2022年中考语文全真模拟试题含解析
- 天津市北辰区名校2022年中考语文考试模拟冲刺卷含解析
- 天津市宁河县市级名校2022年中考一模语文试题含解析
- 扬州市梅岭中学2022年中考一模语文试题含解析