网友您好， 请在下方输入框内输入要搜索的题目：

自学考试专题：工程数学练习题

设A,B均为n阶矩阵,(I一B)可逆,则矩阵方程A＋BX=X的解X=()。


正确答案：(I-B)^(-1)A

n阶正交矩阵的乘积是()矩阵。

A、单位

B、对称

C、实

D、正交


参考答案：D

设N阶矩阵A与对角矩阵合同,则A是().

A.可逆矩阵
B.实对称矩阵
C.正定矩阵
D.正交矩阵

答案：B
解析：

设N阶矩阵A与对角矩阵合同,则A是().

A.可逆矩阵
B.实对称矩阵
C.正定矩阵
D.正交矩阵

答案：B
解析：

设A与B都是n阶正交矩阵，证明AB也是正交矩阵.


答案：
解析：

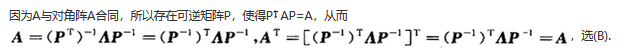
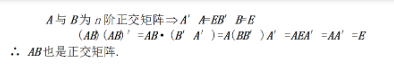
一、选择题1、设、均为阶方阵，则下列命题中不正确的是（ ）。 2、设均为阶方阵且可逆，满足矩阵方程,则下列命题正确的是（ ）。 3、设均为阶正交矩阵，表示的转置矩阵，则下列命题中不正确的是（ ）。是正交矩阵 是正交矩阵 是正交矩阵 是正交矩阵4、排列（1，8，2，7，3，6，4，5）是（ ）。奇排列偶排列非奇非偶以上都不对5、向量组的最大无关组是（ ）。 6、齐次线性方程组有非零解的充分必要条件是（ ）。 7、设向量组，当满足（ ）时，不能由线性表示。 或 8、设，则的特征值是（ ）。 9、齐次线性方程组有非零解，则（ ）。 10、要使都是的解，只要系数矩阵是（ ）。 11、设是非齐次线性方程组的解，是对应的齐次线性方程组的解，则下列结论中正确的是（ ）。 是的解是的解 是的解是的解12、设阶方阵可逆且满足，则必有（ ）。 13、下列命题中正确的是（ ）。设是的解，则是的解设是的解，则是的解设是的解，则是的解设是的解，则是的解14、 设，是任意三个随机事件，则以下命题中正确的是（ ）。15、设，则（ ）。 16、若随机事件两两互不相容，且，则等于（ ）。0.5 0.1 0.44 0.3 17、设随机变量与相互独立，则下列等式中不正确的是（ ）。 18、件新产品中有件次品，现在其中取两次，每次随机地取一件，作不放回抽样，则两件都是正品的概率为（ ）。19、下列命题中不正确的是（ ）。 若，则20、随机变量的方差记为，则下列等式中不正确的是（ ）。（为常数） 21、表示的转置距阵，则下列命题不正确的是（ ）。 22、 （ ）。 23、下列命题中不正确的是（ ）。属于不同特征值的特征向量是线性无关的属于同一特征值的特征向量只有一个两个相似矩阵的特征值相同对称矩阵对应于两个不同特征值的特征向量是正交的24、排列（，）的逆序数为（ ）。25、下列不正确的命题是（ ）。向量组的最大无关组必定唯一向量组的初等变换不改变向量组的秩和向量组的相关性向量组与其最大无关组等价设，若列相关，则行不一定相关26、设使，则的值（ ）。 27、齐次线性方程组有非零解的充分必要条件是常数（ ）。 28、下列命题中正确的是（ ）。若是一组线性相关的维向量，则对于任意不全为的数，均有若是一组线性无关的维向量，则对于任意不全为的数，均有如果向量组中任取个向量所组成的部分向量组都线性无关，则这个向量组本身也是线性无关的若是线性相关的，则其中任何一个向量均可由其余向量线性表示29、（ ）。30、设为n阶方阵，若，则的基础解系中所含向量个数为（ ）。个 个 个 个31、已知向量组线性无关，则下列命题正确的是（ ）。线性无关线性无关线性无关线性无关32、设是阶方阵，则中（ ）。必有两列元素对应成比例 必有一列向量是其余列向量的线性组合任一列向量是其余列向量的线性组合 必有一列向量为零向量33、设为矩阵,则方程组有无穷多解的充要条件是（ ）。 34、 若随机事件和都不发生的概率为，则以下结论正确的是（ ）。 35、 设，则（ ）。 36、下列命题中，正确的是（ ）。 则是不可能事件 则与是互不相容的 则37、方差的充分必要条件是（ ）。 38、设随机变量与相互独立，其概率分布分别为 则下列结论正确的是（ ）。 以上都不正确39、设为随机事件，则下列等式中不正确的是（ ）。 40、设服从两点分布，且，则下列等式中不正确的是（ ）。 41、设,均为阶方阵且可逆，为的行列式,则下列命题中不正确的是（ ）。 42、 （ ）。 43、已知均为阶方阵，则下列命题中正确的是（ ）。 则必有或 的充分条件是或44、 排列（，）是（ ）。 奇排列偶排列非奇非偶以上都不是45、 设为阶方阵，若则的基础解系所含向量个数是（ ） 零个（即不存在）个个个46、（ ） 47、矩阵的特征值是（ ） 48、设是行列式，是元素的代数余子式，下列等式中正确的是（ ） 49、维向量线性无关的充要条件（ ）存在一组不全为的数，使中任意两个向量线性无关中有一个向量不能由其余向量线性表示中任一向量都不能由其余向量线性表示50、 设，均为阶方阵，则下列命题中不正确的是（ ）。 51、 表示向量的长度，则下列命题中不正确的是（ ）。 52、 设是正交矩阵，则下列命题中不正确的是（ ）。 的列向量是两两正交的向量 的行向量都是单位向量且两两相交53、 设表示两向量的内积，为非零向量，下列命题中不正

设A与B都是n阶正交矩阵，证明AB也是正交矩阵.


答案：
解析：

设N阶矩阵A与对角矩阵合同,则A是().

A.可逆矩阵
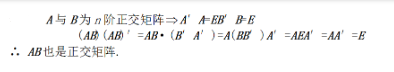
B.实对称矩阵
C.正定矩阵
D.正交矩阵

答案：B
解析：

设A与B都是n阶正交矩阵，证明AB也是正交矩阵.


答案：
解析：

设N阶矩阵A与对角矩阵合同,则A是().

A.可逆矩阵
B.实对称矩阵
C.正定矩阵
D.正交矩阵

答案：B
解析：

设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().

A.矩阵A不可逆
B.矩阵A的迹为零
C.特征值-1,1对应的特征向量正交
D.方程组AX=0的基础解系含有一个线性无关的解向量

答案：C
解析：
由λ1=-1，λ2=0，λ3=1得|A|=0，则r(A)小于3，即A不可逆，(A)正确；又λ1+λ2+λ3=tr(A)=0，所以(B)正确；因为A的三个特征值都为单值，所以A的非零特征值的个数与矩阵A的秩相等，即r(A)=2，从而AX=0的基础解系仅含有一个线性无关的解向量，(D)是正确的；(C)不对，因为只有实对称矩阵的不同特征值对应的特征向量正交，一般矩阵不一定有此性质，所以选(C).

更多 “自学考试专题：工程数学练习题” 相关考题
考题 单选题设A，B都是n阶矩阵。若有可逆矩阵P使得P1AP＝B，则称矩阵A与矩阵B（　　）。A 等价B 相似C 合同D 正交正确答案： B 解析： 相似矩阵的定义：设A、B都是n阶矩阵，若存在可逆矩阵P，使得P－1AP＝B，则称B是A的相似矩阵，知B项正确。
查看答案
考题 设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。A、等价B、相似C、合同D、正交正确答案:B
查看答案
考题 设A是3阶矩阵，P = (α1，α2，α3)是3阶可逆矩阵，且，若矩阵Q=(α2，α1，α3),则Q-1AQ=( )。 答案：B解析：提示：由条件知，λ1=1，λ2=2，λ3=0是矩阵A的特征值,而α1，α2，α3是对应的特征向量，故有。
查看答案
考题 若A，B是正交矩阵，则下列说法错误的是（）。A、AB为正交矩阵B、A+B为正交矩阵C、ATB为正交矩阵D、AB-1为正交矩阵正确答案:B
查看答案
考题 单选题设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。A 等价B 相似C 合同D 正交正确答案： D 解析： 由相似矩阵的定义知B正确。故选B。
查看答案
考题 设A是3阶矩阵，P = (α1，α2，α3)是3阶可逆矩阵，且，若矩阵Q=(α2，α1，α3),则Q-1AQ=( )。 答案：B解析：提示：由条件知，λ1=1，λ2=2，λ3=0是矩阵A的特征值,而α1，α2，α3是对应的特征向量，故有。
查看答案
考题 单选题设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。A 等价B 相似C 合同D 正交正确答案： B 解析： 由相似矩阵的定义知B正确。故选B。
查看答案
考题 单选题若A，B是正交矩阵，则下列说法错误的是（）。A AB为正交矩阵B A+B为正交矩阵C ATB为正交矩阵D AB-1为正交矩阵正确答案： A 解析： 由正交矩阵的定义可知，若A，B正交，则有ATA=I（I为单位阵），BTB=I，则（AB）T（AB）=BTATAB=I，则选项A正确，同理可证明选项C、D也是正交矩阵。而选项B，（A+B）T（A+B）=（AT+BT）（A+B）=2I+BTA+ATB，显然不正确，故选B。
查看答案
考题 单选题设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。A 等价B 相似C 合同D 正交正确答案： C 解析： 由相似矩阵的定义知B正确。故选B。
查看答案
考题 若A，口是正交矩阵，则下列说法错误的是( )。 A、AB为正交矩阵 B、A+B为正交矩阵 C、A-1B为正交矩阵 D、AB-1为正交矩阵 答案：B解析：
查看答案
热门标签
最新考题
最新试卷
热门试卷