网友您好， 请在下方输入框内输入要搜索的题目：

七年级数学下册第五章相交线与平行线周周测8（全章）含答案解析

在液体中作一水平柱面，则其母线为与潜体相切的( )。

A.铅垂线

B.相交线

C.水平线

D.平行线


正确答案：C

在中国北部有这样两个村落，赵村所有的人都是白天祭祀祖先，李庄所有的人都是晚上才祭祀祖先，我们确信没有既在白天也在晚上祭祀祖先的人。我们也知道李明是晚上祭祀祖先的人。

依据以上信息，能断定以下哪项是对李明身份的正确判断?（ ）。

A．李明是赵村的人

B．李明不是赵村的人

C．李明是李庄的人

D．李明不是李庄的人


正确答案：B
虽然李庄所有的人都是晚上才祭祀祖先的，但它的逆命题晚上祭祀祖先的都是李庄的人则不是真命题，又因为赵村的人都是白天祭祀祖先，所以可以推出李明不是赵村的人，至于是不是李庄的，则不能确定。

王某（女）与李某婚后一直未育，李某想收养一个女童。在律师提供的咨询意见中，下列哪一选项是错误的？

A．收养必须经王某同意

B．王某与李某必须年满30周岁

C．收养人不能患有医学上认为不应当收养子女的疾病

D．李某与被收养女童的年龄应当相差40岁以上


正确答案：D

若顺次连接四边形ABCD各边中点所得四边形是矩形，则四边形ABCD一定是( )。

A.对角线相互垂直的四边形
B.矩形
C.对角线相等的四边形
D.菱形

答案：A
解析：
对角线相互垂直的四边形顺次连接各边中点所得四边形是矩形，对角线相等的四边形顺次连接各边中点所得四边形是菱形。

某镇有八个村，其中赵村所有的人都是在白天祭祀祖先，李庄所有的人都是在晚上才祭祀 祖先。现在我们知道李明是晚上祭祀祖先的人。 由此，可以推断（ ）。
A.李明一定是赵村的人
B.李明一定不是赵村的人
C.李明一定是李庄的人
D.李明一定不是李庄的人


答案：B
解析：
考查直言命题的推理。由“赵村所有的人都是在白天祭祀祖先”和“李明 是晚上祭祀祖先的人”可得，李明一定不是赵村的人。但是由“李庄所有的人都是在晚上才祭 祀祖先”和“李明是晚上祭祀祖先的人”推不出李明一定是李庄的人。

第五章 相交线与平行线周周测8一 选择题1.下列选项中能由左图平移得到的是（） A. B. C. D.2.在四边形ABCD中，下列各图中1与2相等的是()3.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在()A.A点 B.B点 C.C点 D.D点4.将命题“对顶角相等”写成“如果，那么”的形式，正确的是（ ）A.如果两个角相等，那么它们是对顶角 B.如果两个角是对顶角，那么它们相等C.如果对顶角，那么相等 D.如果两个角不是对顶角，那么这两个角不相等5.如图，与1是同旁内角的是（） A.2 B.3 C.4 D.56.如图，AB/CD,AGE=128,HM平分EHD,则MHD的度数是（ ） A.46 B.23 C.26 D.247.如图，下列条件中，不能判断直线l1l2的是（ ） A.1=3 B.4=5 C.2=3 D.2+4=1808.如图，直线l1l2，若1=140，2=70，则3的度数是()CA.60 B.65 C.70 D.809.如图，已知ADBC，B=30，DB平分ADE，则DEC=（）A.30 B.60 C.90 D.12010.如图，已知ABDE，ABC=70，CDE=140，则BCD的值为( )A.70 B.50 C.40 D.30二 填空题11.如图，将三角形ABC沿BC方向平移4cm，得到三角形ABC,那么CC= cm.12.将一个直角三角板和一把长方形直尺按如图放置，若=54，则的度数是_.13.如图，把矩形ABCD沿EF对折后使两部分重合，若1=40，则AEF=.14.如图，直线ab，三角板的直角顶点A落在直线a上，两条直角边分别交直线b于B，C两点.若1=42，则2的度数是 .15.如图，ABCD，B=160，D=120，则E=_16.如图：MA1NA2，图：MA1NA3，图：MA1NA4，图：MA1NA5，则第n个图中的A1A2A3An+1= （用含n的代数式表示）.三 解答题17.完成下面的证明：已知，如图，ABCDGH，EG平分BEF，FG平分EFD.求证：EGF=90.证明：HGAB（已知），1=3（_ ）.又HGCD（已知），2=4.ABCD（已知），BEF+_=180（_ ）.又EG平分BEF（已知），1=_.又FG平分EFD（已知），2=_，1+2=（_ ），1+2=90，3+4=90（_ ），即EGF=90.18.如图是一个汉字“互”字，其中，1=2， =.求证：=.19.如图，CDAB于D，点F是BC上任意一点，FEAB于E，且1=2，3=80.（1）证明：B=ADG；（2）求BCA的度数.20.如图，EFAD，ADBC，CE平分BCF，DAC=120，ACF=20，求FEC的度数.21.如图，已知DCFP，1=2，FED=28，AGF=80，FH平分EFG.(1)证明：DCAB；(2)求PFH的度数.22.如图，已知ABCD，C在D的右侧，BM平分ABC，DN平分ADC，BM，DN所在直线交于点E，ADC =70.（1）求EDC的度数；（2）若ABC =n，求BED的度数（用含n的代数式表示）；（3）将线段BC沿DC方向平移， 使得点B在点A的右侧，其他条件不变，画出图形并判断BED的度数是否改变，若改变，求出它的度数（用含n的式子表示）；若不改变，请说明理由.第五章 相交线与平行线周周测8参考答案与解析一、选择题1.C 2.B 3.A 4.B 5.A 6.C 7.C 8.C 9.B 10.D 二、填空题11.4 12.36 13.110 14.48 15.40 16.180n三、解答题17.两直线平行，内错角相等 EFD 两直线平行，同旁内角互补 BEF EFD BEF+EFD 等量代换18.证明：如图，延长交于点.，1=3.又1=2，2=3，HN，=.又=，=. 19.（1）证明：CDAB，FEAB，CDEF， 2=BCD.1=2， 1=BCD，BCDG，B=ADG.（2）解：DGBC， 3=BCA.3=80，BCA=80.20.解：EFAD，ADBC，EFBC，ACB+DAC=180.DAC=120，ACB=60.又ACF=20，FCB=ACBACF=40.CE平分BCF，BCE=20.EFBC，FEC=BCE=20.21.(1) 证明：1=2，ABFP.DCFP，DCAB.(2)解：DCFP，EFP=FED=28.ABFP，GFP=AGF=80.EFG=EFP+GFP=28+80=108.FH平分EFG，EFH=EFG=108=54，PFH=EFH-EFP=54-28=26 .22.解：（1）DE平分ADC，ADC=70，EDC=ADC=70=35.（2）如图，过点E向左作EFAB.ABCD， ABCDEF， ABE=BEF，CDE=DEF.BE平分ABC，DE平分ADC，ABC=n，ADC=70，ABE=ABC=n，CDE=ADC=35，BED=BEF+DEF=n+35. （3）如图，过点E向左作EFAB.BE平分ABC，DE平分ADC，ABC=n，ADC=70，ABE=ABC=n，CDE=ADC=35.ABCD，ABCDEF，BEF=180-ABE=180-n，CDE=DEF=35，BED=BEF+DEF=180-n+35=215-n.图 图如图，过点E向左作EFAB.BM平分ABC，DE平分ADC，ABC=n，ADC=70，ABM=ABC=n，CDE=ADC=35.ABCD，ABCDEF

某镇有八个村．其中赵村所有的人都是在白天祭祀祖先，李庄所有的人都是在晚上才祭祀祖先。现在我们知道李明是晚上祭祀祖先的人。
由此。可以推断（）。
A.李明一定是赵村的人
B.李明一定不是赵村的人
C.李明一定是李庄的人
D.李明一定不是李庄的人


答案：B
解析：
题干申有多个直言命题，考查了直言命题的变形推理和三段论推理。
“赵村所有的人都是在白天祭祀祖先”通过换质得到“赵村所有的人都不是在晚上祭祀祖先”；再通过换位得到“所有在晚上祭祀祖先的人都不是赵村的人”。与“李明是晚上祭祀祖先的人”构成三段论．可推出李明一定不是赵村的人，B项正确。
“李庄所有的人都是在晚上才祭祀祖先”和“李明是晚上祭祀祖先的人”不能构成有效的三段论推理．中项两次不周延，违反了“中项至少周延一次”的规则，故C项不能推出，答案选B。

赵甲、钱乙、孙丙、李丁和周戊分别住在赵楼、钱屯、孙家堡、李庄和周店五个村中，已知：
（1）每个姓氏与所在村庄的第一字不同；
（2）赵甲、孙丙不住李庄；
（3）钱乙不住孙家堡或周店；
（4）李丁不住在赵楼或钱屯；
（5）周戊不住钱屯或赵楼；
（6）除非赵甲住李庄，钱乙才住李庄；
（7）若赵甲住孙家堡，则孙丙住李庄。
根据以上信息可得出：

A.李丁住孙家堡
B.钱乙住李庄
C.孙丙住周店
D.赵甲住钱屯

答案：A
解析：
第一步，确定题型。
题干具有匹配特征，确定为分析推理。
第二步，分析条件，进行推理。
根据题干，横向是村，纵向是人，根据（1）每个姓氏与所在村庄的第一字不同，如图：

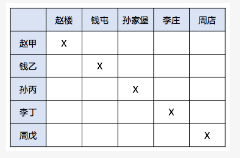
根据（2）赵甲、孙丙不住李庄（3）钱乙不住孙家堡或周店（4）李丁不住在赵楼或钱屯（5）周戊不住钱屯或赵楼，如图：

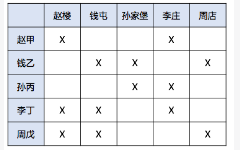
根据（6）钱乙李庄→赵甲李庄，（2）“赵甲不住李庄”，根据否后必必否前，得到“钱乙不住李庄”；再根据（7）赵甲孙家堡→孙丙李庄，（2）“孙丙不住李庄”，根据否后必必否前，得到“赵甲不住孙家堡”，如图：

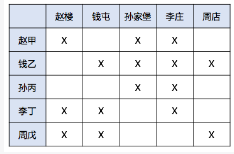
由此可得，周戊住李庄，如图：

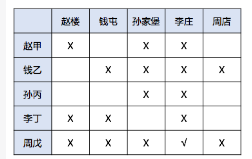
再将可确定的信息全部填入表格，如图：

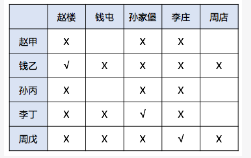
根据上表，赵甲和孙丙无法确定，李家住在孙家堡。
因此，选择A选项。

王某借给周某10万元，由李某和蒋某提供保证担保，王某与李某、蒋某约定，李某和蒋某各保证5万元的清偿。下列说法正确的是()。

A.若周某不能按时还款，李某和蒋某对周某的债务承担按份责任
B.若李某和蒋某之间关于保证份额的约定并未取得王某的同意，则李某和蒋某对周某的债务承担连带责任
C.若李某和蒋某约定各承担50%的保证份额约定并没有得到王某的同意，这个约定只能在李某和蒋某之间有效
D.若周某不能按时还款，王某只能向李某或蒋某中的一人主张权利

答案：A,B,C
解析：
按份责任与连带责任是对共同责任的区分。连带责任是共同责任人对全部债务的承担具有连带关系的责任。按份责任又被称为分割责任，是共同责任人按照法律的规定或者合同的约定各自承担一定份额的责任。对于按份责任，债权人只能按照份额向债务人主张权利。所以D项的说法是错误的。因此，本题选ABC。

王某借给周某10万元，由李某和蒋某提供保证担保，王某与李某、蒋某约定，李某和蒋某各保证5万元的清偿。下列说法正确的是()。

A.若周某不能按时还款，李某和蒋某对周某的债务承担按份责任
B.若李某和蒋某之间关于保证份额的约定并未取得王某的同意，则李某和蒋某对周某的债务承担连带责任
C.若李某和蒋某约定各承担50%的保证份额约定并没有得到王某的同意，这个约定只能在李某和蒋某之间有效
D.若周某不能按时还款，王某只能向李某或蒋某中的一人主张权利

答案：A,B,C
解析：
按份责任与连带责任是对共同责任的区分。连带责任是共同责任人对全部债务的承担具有连带关系的责任。按份责任又被称为分割责任，是共同责任人按照法律的规定或者合同的约定各自承担一定份额的责任。对于按份责任，债权人只能按照份额向债务人主张权利。所以D项的说法是错误的。因此，本题选ABC。

王某借给周某10万元，由李某和蒋某提供保证担保，王某与李某、蒋某约定，李某和蒋某各保证5万元的清偿。下列说法正确的是()。

A.若周某不能按时还款，李某和蒋某对周某的债务承担按份责任
B.若李某和蒋某之间关于保证份额的约定并未取得王某的同意，则李某和蒋某对周某的债务承担连带责任
C.若李某和蒋某约定各承担50%的保证份额约定并没有得到王某的同意，这个约定只能在李某和蒋某之间有效
D.若周某不能按时还款，王某只能向李某或蒋某中的一人主张权利

答案：A,B,C
解析：
按份责任与连带责任是对共同责任的区分。连带责任是共同责任人对全部债务的承担具有连带关系的责任。按份责任又被称为分割责任，是共同责任人按照法律的规定或者合同的约定各自承担一定份额的责任。对于按份责任，债权人只能按照份额向债务人主张权利。所以D项的说法是错误的。因此，本题选ABC。

更多 “七年级数学下册第五章相交线与平行线周周测8（全章）含答案解析” 相关考题
考题 李庄古镇的位置是在长江边正确答案:正确
查看答案
考题 赵甲、钱乙、孙丙、李丁和周戊分别住在赵楼、钱屯、孙家堡、李庄和周店五个村中，已知： （1）每个姓氏与所在村庄的第一字不同； （2）赵甲、孙丙不住李庄； （3）钱乙不住孙家堡或周店； （4）李丁不住在赵楼或钱屯； （5）周戊不住钱屯或赵楼； （6）除非赵甲住李庄，钱乙才住李庄； （7）若赵甲住孙家堡，则孙丙住李庄。 根据以上信息可得出：A.李丁住孙家堡 B.钱乙住李庄 C.孙丙住周店 D.赵甲住钱屯答案：A解析：第一步，确定题型。 题干具有匹配特征，确定为分析推理。 第二步，分析条件，进行推理。 根据题干，横向是村，纵向是人，根据（1）每个姓氏与所在村庄的第一字不同，如图： 根据（2）赵甲、孙丙不住李庄（3）钱乙不住孙家堡或周店（4）李丁不住在赵楼或钱屯（5）周戊不住钱屯或赵楼，如图： 根据（6）钱乙李庄→赵甲李庄，（2）“赵甲不住李庄”，根据否后必必否前，得到“钱乙不住李庄”；再根据（7）赵甲孙家堡→孙丙李庄，（2）“孙丙不住李庄”，根据否后必必否前，得到“赵甲不住孙家堡”，如图： 由此可得，周戊住李庄，如图： 再将可确定的信息全部填入表格，如图： 根据上表，赵甲和孙丙无法确定，李家住在孙家堡。 因此，选择A选项。
查看答案
考题 王某(女)与李某婚后一直未育，李某想收养一个女童。在律师提供的咨询意见中，下列选项错误的是（） A.收养必须经王某同意 B.王某与李某必须年满30周岁 C.收养人不能患有医学上认为不应当收养子女的疾病 D.李某与被收养女童的年龄应当相差40岁以上答案：D解析：【考情点拨】本题考查了收养人条件的知识点。 【应试指导】《收养法》第6条规定，收养人应当同时具备下列条件：(1)无子女；(2)有抚养教育被收养人的能力；(3)未患有在医学上认为不应当收养子女的疾病；(4)年满30周岁。第9条规定，无配偶的男性收养女性的，收养人与被收养人的年龄应当相差40周岁以上。第10条第2款规定，有配偶者收养子女，须夫妻共同收养。故A、B、C三项的说法都是正确的，D项错误。
查看答案
考题 王某借给周某10万元，由李某和蒋某提供保证担保，王某与李某、蒋某约定，李某和蒋某各保证5万元的清偿。下列说法正确的是()。A.若周某不能按时还款，李某和蒋某对周某的债务承担按份责任 B.若李某和蒋某之间关于保证份额的约定并未取得王某的同意，则李某和蒋某对周某的债务承担连带责任 C.若李某和蒋某约定各承担50%的保证份额约定并没有得到王某的同意，这个约定只能在李某和蒋某之间有效 D.若周某不能按时还款，王某只能向李某或蒋某中的一人主张权利答案：A,B,C解析：按份责任与连带责任是对共同责任的区分。连带责任是共同责任人对全部债务的承担具有连带关系的责任。按份责任又被称为分割责任，是共同责任人按照法律的规定或者合同的约定各自承担一定份额的责任。对于按份责任，债权人只能按照份额向债务人主张权利。所以D项的说法是错误的。因此，本题选ABC。
查看答案
考题 王某借给周某10万元，由李某和蒋某提供保证担保，王某与李某、蒋某约定，李某和蒋某各保证5万元的清偿。下列说法正确的是()。A.若周某不能按时还款，李某和蒋某对周某的债务承担按份责任 B.若李某和蒋某之间关于保证份额的约定并未取得王某的同意，则李某和蒋某对周某的债务承担连带责任 C.若李某和蒋某约定各承担50%的保证份额约定并没有得到王某的同意，这个约定只能在李某和蒋某之间有效 D.若周某不能按时还款，王某只能向李某或蒋某中的一人主张权利答案：A,B,C解析：按份责任与连带责任是对共同责任的区分。连带责任是共同责任人对全部债务的承担具有连带关系的责任。按份责任又被称为分割责任，是共同责任人按照法律的规定或者合同的约定各自承担一定份额的责任。对于按份责任，债权人只能按照份额向债务人主张权利。所以D项的说法是错误的。因此，本题选ABC。
查看答案
考题 在“平行线的性质”的新授课上，一位教师设计了如下的教学片段：一、复习 1．如何用同位角、内错角、同旁内角来判定两条直线是否平行? 2．把它们已知和结论颠倒一下，可得到怎样的语句?"它们正确吗?二、新授 1．实验观察．发现平行线第一个性质。 在此基础上指出：“平行线的性质2(定理)”和“平行线的性质3(定理)”。3．平行线判定与性质的区别与联系。 投影：将判定与性质各三条全部打出。 ? ? (1)性质：根据两条直线平行，去证角的相等或互补。(2)判定：根据两角相等或互补，去证两条直线平行。联系是：它们的条件和结论是互逆的。性质与判定要证明的问题是不同的。 ? ? 针对上述材料，完成下列任务。 ? ? (1)本教学片段运用什么导入方法?并简述这种导入方法的优点。(7分) ? ?(2)简述本节课内容的教学目标。(5分) ? ? (3)本节课的重点和难点分别是什么?(5分) ? ? (4)为了进一步巩固平行线的性质定理，请设计相应例题和习题各一个，并写明解题思路。(13分)答案：解析：(1)本教学片段运用了复习导人。这种导入方法利用新旧知识间的逻辑联系，即旧知识是新知识的基础，新知识是旧知识的发展与延伸，从而找出新旧知识联结的交点，由旧知识的复习迁移到新知识的学习上来导入新课。通过这种方法导入新课可以淡化学生对新知识的陌生感，使学生迅速将新知识纳入原有的知识结构中，能有效降低学生对新知识的认知难度。 (2)①理解平行线的性质和判定的区别： ②掌握平行线的三个性质，并能运用它们作简单的推理。(3)重点：平行线的三个性质。 难点：平行线的三个性质和怎样区分性质定理和判定定理。 (4)例题：如图所示，已知：AD／／BC，∠AEF=∠B，求证：AD／／EF。 分析：(执果索因)从图直观分析，欲证AD／／只需∠A＋∠EF=1800 (由因求果)因为AD／／BC，所以∠A+∠B=1800，又∠B=∠AEF，所以∠A＋∠AEF=180。成立。于是得证。 证明：因为AD／／BC． 所以∠A+∠B=1800。(两直线平行，同旁内角互补)因为￡AE聘[曰，(已知) 所以∠A+∠AEF=1800，(等量代换) 所以AD／／EF.(同旁内角互补，两条直线平行) 练习：如图所示，已知：AE平分∠BAC，C E ，且AB／／CD。且AB∥CD 求证：∠l+∠2＝900。 证明：因为AB／／CD． 所以∠BAC+∠ACD＝1800． 又因为AE平分∠BAC，CE平分∠ACD，
查看答案
考题 单选题A、B、C三支施工队在王庄和李庄修路，王庄要修路900米，李庄要修路1250米。已知A、B、C队每天分别能修24米、 30米、32米，A、C队分别在王庄和李庄修路，B队先在王庄，施工若干天后转到李庄，两地工程同时开始同时结束。问B队在王庄工 作了几天：A 9 B 10 C 11 D 12正确答案： D 解析：
查看答案
考题 某位教师在讲完《相交线与平行线》这部分内容后，设计了一节《相交线与平行线》的复习课，在这节课中他设计了如下一组题： 题1、如图3，BE平分∠ABD，DE平分∠BDC且∠1+∠2=90°。 ①BE与DE有什么样的位置关系？说明理由。 ②AB与CD有什么样的位置关系？说明理由。 阅读上述教学设计片段，完成下列任务： （1）从这组习题分析这节复习课的教学目标；（8分） （2）分析这三道题的设计意图，并说明习题设计的特点（10分） （3）请你在图5的基础上，编一道类似习题，并给出答案（12分）答案：解析：本题主要以初中数学 “相交线与平行线”的复习课为例，考查相交线与平行线的基础知识、课程的内容标准及有效数学教学等相关知识，比较综合性地考查学科知识、课程知识以及教学技能的基本知识和基本技能。 （1）复习课的教学目标也要是新课标倡导的三维教学目标，即知识与技能目标、过程与方法目标、情感态度与价值观目标。知识与技能目标，是对学生学习结果的描述，即学生同学习所要达到的结果，又叫结果性目标。这种目标一般有三个层次的要求：学懂、学会、能应用。 （2）第一题，结合角平分线的性质，巩固两直线平行判定定理的应用。第二题在第一题的基础上进行变形，利用两直线平行的性质求角的度数，巩固两直线平行性质的应用。第三题是在前两题的基础上，将具体角变抽象角，进行猜想、探索证明，加深巩固学生对两直线平行的性质的应用，提高学生合理推理和演绎推理能力，将所学知识融会贯通。三道题目逻辑联系紧密，遵循逐进，步步深入，以达到了能够所学知识灵活运用并初步形成几何直观，发展形象思维与抽象思维，锻炼合情推理和演绎推理能力的目的。 （3）在图5的基础上，结合题3编一道类似习题，合情合理即可，并给出答案。
查看答案
考题 写出分属于下列科的校园植物。 李亚科1.（）2.（）3.（） 苹果亚科1.（）2.（）3.（） 绣线菊亚科1.（）2.（） 蔷薇亚科（） 十字花科1.（）2.（） 藜科1.（）2.（） 蓼科（） 堇菜科（） 卫矛科（） 蝶形花科1.（）2.（）3.（）正确答案:杏；李；桃；苹果；梨；山楂；珍珠梅；风箱果；玫瑰；独行菜；荠菜；猪毛菜；藜；巴天酸模；早开堇菜；桃叶卫矛；刺槐；紫花苜蓿；披针叶黄华
查看答案
考题 某位教师在讲完《相交线与平行线》这部分内容后，设计了一节《相交线与平行线》的复习课．在这节课中，他设计了如下一组题： 题1．如图3．BE平分∠ABD，DE平分∠BDC，且∠1+∠2=90。。 ①BE与DE有什么样的位置关系 请说明理由。 ②AB与CD有什么样的位置关系 请说明理由。 题2．如图4，AB∥CD且∠1+∠2=800：，求∠BED的度数。 题3．如图5，AB∥CD直线1交AB于点F、交CD于点G，点E是线段GF上的一点(点E 与点F、G不重合)，设∠ABC＝β,∠BED=γ。试探索a，β、γ之间的关系，并说明理由。 阅读上述教学设计片段，完成下列任务： (1)从这组习题分析这节复习课的教学目标；(8分) (2)分析这三道题的设计意图，并说明这组习题设计的特点；(10分) (3)请你在图5的基础上，编一道类似习题，并给出答案。(12分) 答案：解析：(1)知识与技能目标：能够利用平行线的性质与判定定理，判断两条直线是否平行；能够利用两直线相交的性质求相交直线的交角度数。 过程与方法目标：学生通过对两直线的位置关系进行观察、猜想、探索等过程，初步形成几何直观，发展形象思维与抽象思维．锻炼合情推理和演绎推理能力，并能清晰地表达自己的想法。 情感态度与价值观目标：在学习过程中，体验获得成功的乐趣，锻炼克服困难的意志，建立自信心。养成认真勤奋、独立思考、合作交流、反思质疑等学习习惯，形成实事求是的科学态度。 (2)第一道题目，给出已知条件BE平分厶4BD，DE平分L_BDC且∠1+∠2=90。，通过两个问题引导学生思考，利用角平分线的性质，先判断出BE与DE的位置关系，进而利用两直线平行的判定定理判断AB与CD的位置。这道题目结合学生的已有知识经验，加深巩固对两直线平行判定定理的应用。为第三道题目的猜想做铺垫。 第二道题目．在第一道题目的基础之上对题目进行变形，已知AB∥CD且∠l+∠2=80。，结合对一道题目解题的经验，利用两直线平行的性质求出∠BED的度数。这道题目的主要设计意图为加深巩固学生对两直线平行的性质的应用，并为第三道题目的猜想做铺垫。 第三道题目。在前两道题目的铺垫下，将具体角变为抽象角，学生结合前两道题目的解题经验，进行猜想、探索证明。这道题目的主要设计意图为加深巩固学生对两直线平行的性质的应用，提高学生合情推理和演绎推理能力，将所学知识融会贯通。 三道题目逻辑联系紧密，考虑到学生的认知顺序，遵循由浅入深，由易到难，由表及里等一系列规律，让学生能够拾级而上，循序渐进，步步深入。以达到能够将所学知识灵活运用并初步形成几何直观，发展形象思维与抽象思维，锻炼合情推理和演绎推理能力的目的。 (3)如图5，直线l交AB于点F、交CD于点G，点E是线段GF上的一点(点E与点F、G不重合)，设∠ABE=01，∠CDE=fl，LBED=y。试探索γβα满足何条件的时候，AB与CD平行，并说明理由。 当a+B＝Y时，AB与CD平行。连接BD，因为三角形BDE的内角和为180度，所以∠EBD+∠EDB=1800一∠BDE，若β+α=γ，则∠EBD+∠EDB+α+β=1800～∠BED+α+β=1800，则AB与CD平行。
查看答案
热门标签
最新考题
最新试卷
热门试卷