网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
某位教师在讲完《相交线与平行线》这部分内容后,设计了一节《相交线与平行线》的复习课,在这节课中他设计了如下一组题:
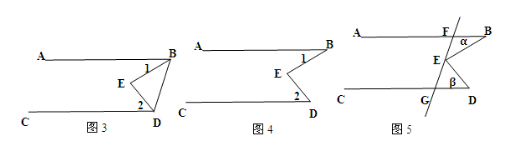
题1、如图3,BE平分∠ABD,DE平分∠BDC且∠1+∠2=90°。
①BE与DE有什么样的位置关系?说明理由。
②AB与CD有什么样的位置关系?说明理由。

阅读上述教学设计片段,完成下列任务:
(1)从这组习题分析这节复习课的教学目标;(8分)
(2)分析这三道题的设计意图,并说明习题设计的特点(10分)
(3)请你在图5的基础上,编一道类似习题,并给出答案(12分)
题1、如图3,BE平分∠ABD,DE平分∠BDC且∠1+∠2=90°。
①BE与DE有什么样的位置关系?说明理由。
②AB与CD有什么样的位置关系?说明理由。


阅读上述教学设计片段,完成下列任务:
(1)从这组习题分析这节复习课的教学目标;(8分)
(2)分析这三道题的设计意图,并说明习题设计的特点(10分)
(3)请你在图5的基础上,编一道类似习题,并给出答案(12分)
参考答案
参考解析
解析:本题主要以初中数学 “相交线与平行线”的复习课为例,考查相交线与平行线的基础知识、课程的内容标准及有效数学教学等相关知识,比较综合性地考查学科知识、课程知识以及教学技能的基本知识和基本技能。
(1)复习课的教学目标也要是新课标倡导的三维教学目标,即知识与技能目标、过程与方法目标、情感态度与价值观目标。知识与技能目标,是对学生学习结果的描述,即学生同学习所要达到的结果,又叫结果性目标。这种目标一般有三个层次的要求:学懂、学会、能应用。
(2)第一题,结合角平分线的性质,巩固两直线平行判定定理的应用。第二题在第一题的基础上进行变形,利用两直线平行的性质求角的度数,巩固两直线平行性质的应用。第三题是在前两题的基础上,将具体角变抽象角,进行猜想、探索证明,加深巩固学生对两直线平行的性质的应用,提高学生合理推理和演绎推理能力,将所学知识融会贯通。三道题目逻辑联系紧密,遵循逐进,步步深入,以达到了能够所学知识灵活运用并初步形成几何直观,发展形象思维与抽象思维,锻炼合情推理和演绎推理能力的目的。
(3)在图5的基础上,结合题3编一道类似习题,合情合理即可,并给出答案。
(1)复习课的教学目标也要是新课标倡导的三维教学目标,即知识与技能目标、过程与方法目标、情感态度与价值观目标。知识与技能目标,是对学生学习结果的描述,即学生同学习所要达到的结果,又叫结果性目标。这种目标一般有三个层次的要求:学懂、学会、能应用。
(2)第一题,结合角平分线的性质,巩固两直线平行判定定理的应用。第二题在第一题的基础上进行变形,利用两直线平行的性质求角的度数,巩固两直线平行性质的应用。第三题是在前两题的基础上,将具体角变抽象角,进行猜想、探索证明,加深巩固学生对两直线平行的性质的应用,提高学生合理推理和演绎推理能力,将所学知识融会贯通。三道题目逻辑联系紧密,遵循逐进,步步深入,以达到了能够所学知识灵活运用并初步形成几何直观,发展形象思维与抽象思维,锻炼合情推理和演绎推理能力的目的。
(3)在图5的基础上,结合题3编一道类似习题,合情合理即可,并给出答案。
更多 “某位教师在讲完《相交线与平行线》这部分内容后,设计了一节《相交线与平行线》的复习课,在这节课中他设计了如下一组题: 题1、如图3,BE平分∠ABD,DE平分∠BDC且∠1+∠2=90°。 ①BE与DE有什么样的位置关系?说明理由。 ②AB与CD有什么样的位置关系?说明理由。 阅读上述教学设计片段,完成下列任务: (1)从这组习题分析这节复习课的教学目标;(8分) (2)分析这三道题的设计意图,并说明习题设计的特点(10分) (3)请你在图5的基础上,编一道类似习题,并给出答案(12分)” 相关考题
考题
初中数学《平行线的判定》
一、考题回顾
二、考题解析
【教学过程】
(一)引入新课
提出问题:回忆上节课我们学过的平行线的定义是什么?
(二)探索新知
学生活动:回忆平行线的定义:
提问1:由于直线的无限延伸检验是否相交有困难,那么有没有其他判定方法呢?
回忆用直尺和三角尺作平行线方法,引导学生探究三角尺起着怎么样的作用。
共同总结:利用三角尺的实质就是做了相等的同位角。
教师明确:也就是说,两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行,简单说成:同位角相等,两直线平行。
提问2:思考木工用图中的角尺画平行线的道理。
学生活动:自主探究木工画平行线的道理。
提问3:两条直线被第三条直线所截同时得到同位角相等、内错角相等、同旁内角互补,那么既然有了同位角相等两直线平行,可否通过内错角相等或者同旁内角互补来证明两直线平行呢?
学生活动:小组探究。
师生归纳总结:平行线判定的另两种方法即内错角相等,两直线平行;同旁内角互补,两直线平行。
(三)课堂练习
练习题1和练习题2。
(四)小结作业
提问:今天有什么收获?
引导学生回顾:本节课学习的平行线的判定的三种方法。
课后作业:
思考:到目前为止,我们学习过多少种方法可以判定两直线平行。
【板书设计】
【答辩题目解析】
1.截止到目前,学生掌握的平行线的判定有几种方法?
2.在本节课的教学过程中,你是如何设计的?
考题
某位教师在讲完《相交线与平行线》这部分内容后,设计了一节《相交线与平行线》的复习课,在这节课中他设计了如下一组题:
题1、如图3,BE平分∠ABD,DE平分∠BDC且∠1+∠2=90°。
①BE与DE有什么样的位置关系?说明理由。
②AB与CD有什么样的位置关系?说明理由。
阅读上述教学设计片段,完成下列任务:
(1)从这组习题分析这节复习课的教学目标;(8分)
(2)分析这三道题的设计意图,并说明习题设计的特点(10分)
(3)请你在图5的基础上,编一道类似习题,并给出答案(12分)
考题
在“平行线的性质”的新授课上,一位教师设计了如下的教学片段:一、复习
1.如何用同位角、内错角、同旁内角来判定两条直线是否平行?
2.把它们已知和结论颠倒一下,可得到怎样的语句?"它们正确吗?二、新授
1.实验观察.发现平行线第一个性质。
在此基础上指出:“平行线的性质2(定理)”和“平行线的性质3(定理)”。3.平行线判定与性质的区别与联系。
投影:将判定与性质各三条全部打出。
? ? (1)性质:根据两条直线平行,去证角的相等或互补。(2)判定:根据两角相等或互补,去证两条直线平行。联系是:它们的条件和结论是互逆的。性质与判定要证明的问题是不同的。
? ? 针对上述材料,完成下列任务。
? ? (1)本教学片段运用什么导入方法?并简述这种导入方法的优点。(7分)
? ?(2)简述本节课内容的教学目标。(5分)
? ? (3)本节课的重点和难点分别是什么?(5分)
? ? (4)为了进一步巩固平行线的性质定理,请设计相应例题和习题各一个,并写明解题思路。(13分)
考题
某位教师在讲完《相交线与平行线》这部分内容后,设计了一节《相交线与平行线》的复习课.在这节课中,他设计了如下一组题:
题1.如图3.BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90。。
①BE与DE有什么样的位置关系 请说明理由。
②AB与CD有什么样的位置关系 请说明理由。
题2.如图4,AB∥CD且∠1+∠2=800:,求∠BED的度数。
题3.如图5,AB∥CD直线1交AB于点F、交CD于点G,点E是线段GF上的一点(点E
与点F、G不重合),设∠ABC=β,∠BED=γ。试探索a,β、γ之间的关系,并说明理由。
阅读上述教学设计片段,完成下列任务:
(1)从这组习题分析这节复习课的教学目标;(8分)
(2)分析这三道题的设计意图,并说明这组习题设计的特点;(10分)
(3)请你在图5的基础上,编一道类似习题,并给出答案。(12分)
考题
单选题一位教师在一节市级示范课中准备得很充分,没想到在实际课堂中学生表现得非常拘谨,不敢举手回答问题,一节课结束,有的学生还没有完全学会这首歌。这位老师自我反思,觉得教学设计存在的问题是关键,关注了如何“教”,忽略了学生的“学”,没有留给学生自主探究的空间。请问,这属于教学反思的()。A
课前反思B
课后反思C
课中反思D
持续反思
考题
单选题空间直线根据其与投影面的相对位置关系可以分为三类,它们是()。A
正平线、水平线、侧平线B
正垂线、铅垂线、侧垂线C
一般位置线、投影面平行线、投影面垂直线D
平行线、相交线、异面线
考题
判断题在黎曼几何中,两条平行线是永不相交的。A
对B
错
热门标签
最新试卷