网友您好, 请在下方输入框内输入要搜索的题目:
请你写出一个有一根为1的一元二次方程:____________.
19世纪60年代,麦克斯韦列出了表达电磁基本定律的()
A 、一元方程式
B 、一元二次方程组
C 、四元方程组
D 、二元二次方程组
如果2是一元二次方程x2+bx+2=0的一个根,那么常数b的值为________________.
-3
一元二次方程x2+x-2=0 的两根之积是( )
A.-1
B.-2
C.1
D.2
一、考题回顾

【教学过程】
(一)引入新课
复习回顾一元二次方程的一般形式以及求根公式。
提出问题:一元二次方程的根与方程中的系数之间有怎样的关系呢?
引出课题。

(四)小结作业
提问:今天有什么收获?引导学生回顾:一元二次方程根与系数的关系以及推导证明过程。
作业:课后练习。
【板书设计】

【答辩题目解析】
1.教学目标是什么?
【参考答案】
(1)知识与技能
学生知道一元二次方程根与系数的关系,并会应用根与系数关系解决问题。
(2)过程与方法
学生能够借助问题的引导,发现、归纳并证明一元二次方程根与系数的关系,在探究过程中,感受由特殊到一般地认识事物的规律。
(3)情感态度价值观
通过探索一元二次方程的根与系数的关系,激发发现规律的积极性,鼓励勇于探索的精神。

1一元二次方程课时学案(一)元二次方程 【目标导航】1、经历由实际问题抽象出一元二次方程的过程,进一步体会方程是刻画现实世界的有效数学模型;2、了解一元二次方程的概念和它的一般形式 bx+c= 0(a0) ,正确理解和掌握一般形式中的 a0, “项” 和“系数”等概念;会根据实际问题列一元二次方程;一、磨刀不误砍柴工,上新课之前先来热一下身吧!1、下列方程:(1)x 2; (2)4 x2+; (3)(0; (4)=3 (5) 其中,一元二次方程有( )32 个 B2 个 C3 个 D4 个2、一元二次方程(x+1) (310 的一般形式是 ,二次项 ,二次项系数 ,一次项 ,一次项系数 ,常数项 。二、牛刀小试正当时,课堂上我们来小试一下身手!3、小区在每两幢楼之间,开辟面积为 900 平方米的一块长方形绿地,并且长比宽多 10米,则绿地的长和宽各为多少?4、一个数比另一个数大 3,且两个数之积为 10,求这两个数。5、下列方程中,关于 x 的一元二次方程是( )A.3(x+1)2= 2(x+1) B. 0512bx+c= 0 x= 6、把下列方程化成 bx+c= 0 的形式,写出 a、b、c 的值:(1)37 (2)3( = 2(47、当 m 为何值时,关于 x 的方程(x 2=关于 x 的一元二次方程?8、若关于的方程(x a2 是一元二次方程,求 a 的值?三、新知识你都掌握了吗?课后来这里显显身手吧!9、一个正方形的面积的 2 倍等于 15,这个正方形的边长是多少?10、一块面积为 600 平方厘米的长方形纸片,把它的一边剪短 10 厘米,恰好得到一个正方形。求这个正方形的边长。211、判断下列关于 x 的方程是否为一元二次方程:(1)2(x 21) =3y;
一、考题回顾

二、考题解析
【教学过程】
(一)引入新课
复习旧知:回顾之前学习过哪些方程,并对一元一次方程的定义进行回顾。
总结:明确本节课学习初中阶段的最后一种方程,《一元二次方程》。

【板书设计】

【答辩题目解析】
1.谈一谈你本节课导入的设计意图是什么?
2.一元二次方程、二次函数、一元二次不等式之间的联系是什么?
这样的设计既可以考察学生对之前知识的掌握情况,还能够为今天学习一元二次方程的概念打下基础。
2、三者之间联系非常的紧密:一元二次方程的根为二次函数与x轴交点的横坐标;一元二次不等式的解集其中大于0的部分为二次函数在x轴上方函数图象的定义域,小于0部分为二次函数在x轴下方函数图象的定义域。
【教师甲】
设置问题:请同学们根据下列问题,只列出含未知数的方程:

预设:学生会分别列出两个方程。
教师要求学生分别整理成方程左侧降幂排序,右侧为零的形式,然后引导学生完成下面两件事:对比“一元一次方程”的定义,为这类方程定义一个名称——一元二次方程。再请学生自行写出几个不同的一元二次方程,并提炼出一元二次方程的一般表达式。
【教师乙】
上课开始。提问:什么是“一元一次方程”?请你根据“一元一次方程”的定义,给出“一元二次方程”的定义,并举出几个“一元二次方程”的例子。在学生举例的基础上,提炼出“一元二次方程”的一般表达式。
请完成下列任务:
(1)请分析两位老师引入“一元二次方程”概念设计方案的各自的特点。(15分)
(2)在教学中,当引入一个新的数学概念之后,往往通过例题、习题加深对概念的理解。请针对“一元二次方程”概念,设计不同难度的两道例题和两道练习题,加深学生对“一元二次方程”概念的理解。(15分)
(1)教学活动是师生积极参与、交往互动、共同发展的过程。有效的教学活动是学生学与教师教的统一,学生是学习的主体,教师是学习的组织者、引导者和合作者。数学教学活动应激发学生的学习兴趣,调动学生积极性,引发学生思考,鼓励学生的创造性思维。在教学的过程中教师应培养学生良好的数学学习习惯,使学生掌握恰当的数学学习方法。也注重以学生的认知发展水平和已有经验为基础,面向全体学生,采取启发式和因材施教的教学。学生在生动活泼的、主动的教学课堂中,更容易吸收知识,但也应注重多种学习方式相结合,除接受学习外,动手实践、主动探索与合作交流同样是学习数学的重要方式。
教师甲的教学方案,相对于乙教师来说,更加非常符合素质教育的要求。
(2)针对“一元二次方程”概念,设计不同难度的两道例题和两道练习题,题目的难度应适当,目的是加深学生对“一元二次方程”概念的理解。
①进一步了解一元二次方程的概念;
②进一步了解-元二次方程的多种解法(配方法、公因式法、因式分解法等);
③会运用判别式判断一元二次方程根的情况;
④通过相关问题的讨论,在理解相关知识的同时,休会数学思想方法,积累数学活动经验。 问题:
根据上述教学目标,完成下列任务:
(1)为了落实上述教学目标①、②,请设计一个教学片段,并说明设计意图;
(2)配方法是解一元二次方程的通性解法,请设计问题串,以帮助学生进一步理解配方法在解一元二次方程中的作用。


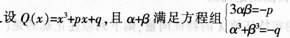 (1)证明α+β是Q(χ)=0的根;(3分)
(1)证明α+β是Q(χ)=0的根;(3分)
(2)写出以α3和β3为根的一元二次方程。(4分)

【教师甲】
设置问题:请同学们根据下列问题,只列出含未知数的方程:
(1)一个正方形的面积为2,求正方形的边长x。

预设:学生会分别列出两个方程。
教师要求学生分别整理成方程左侧降幂排序,右侧为零的形式,然后引导学生完成下面两件事:对比“一元一次方程”的定义,为这类方程定义一个名称——一元二次方程。再请学生自行写出几个不同的一元二次方程,并提炼出一元二次方程的一般表达式。
【教师乙】
上课开始。提问:什么是“一元一次方程”?请你根据“一元一次方程”的定义,给出“一元二次方程”的定义,并举出几个“一元二次方程”的例子。在学生举例的基础上,提炼出“一元二次方程”的一般表达式。
请完成下列任务:
(1)请分析两位老师引入“一元二次方程”概念设计方案的各自的特点。(15分)
(2)在教学中,当引入一个新的数学概念之后,往往通过例题、习题加深对概念的理解。请针对“一元二次方程”概念,设计不同难度的两道例题和两道练习题,加深学生对“一元二次方程”概念的理解。(15分)
(1)教学活动是师生积极参与、交往互动、共同发展的过程。有效的教学活动是学生学与教师教的统一,学生是学习的主体,教师是学习的组织者、引导者和合作者。数学教学活动应激发学生的学习兴趣,调动学生积极性,引发学生思考,鼓励学生的创造性思维。在教学的过程中教师应培养学生良好的数学学习习惯,使学生掌握恰当的数学学习方法。也注重以学生的认知发展水平和已有经验为基础,面向全体学生,采取启发式和因材施教的教学。学生在生动活泼的、主动的教学课堂中,更容易吸收知识,但也应注重多种学习方式相结合,除接受学习外,动手实践、主动探索与合作交流同样是学习数学的重要方式。
教师甲的教学方案,相对于乙教师来说,更加非常符合素质教育的要求。
(2)针对“一元二次方程”概念,设计不同难度的两道例题和两道练习题,题目的难度应适当,目的是加深学生对“一元二次方程”概念的理解。
更多 “17页一元二次方程同步学案含答案” 相关考题
- 简述嫡长子继承制的含义及意义。
- 商王掌握商朝的最高司法权,他利用()假借天意断案。
- 炼铁厂带煤气作业的类别是如何划分的?
- 对交通肇事构成犯罪,依法应当吊销驾驶人机动车驾驶证的,应当在(),由设区市公安机关交通管理部门依法吊销机动车驾驶证。A、送达事故认定书之日起五日内B、损害赔偿调解结束之日起五日内C、移送人民检察院审查起诉以前D、人民法院作出有罪判决后
- 公安信息录入的流程包括()。A、整理B、输录C、检查D、分析
- 元朝地方司法体系有如下几级()。A、路B、州C、县D、府
- 元律不禁止“同姓通婚”,因为蒙古人、色目人盛行婚姻自由的思想,故对同姓通婚不加限制。
- 国家对以下哪类企业实行安全生产许可制度?()A、家电销售企业B、运输企业C、建筑施工企业
- 公安交通管理信息系统建设成效是什么?
- 对起重机制动器的要求是什么?