网友您好， 请在下方输入框内输入要搜索的题目：

[原创]2021年数学一轮复习精品试题第50讲 古典概型与几何概型

二、填空题(本大题共15小题，每小题2分，共30分)

请在每小题的空格中填上正确答案。错填、不填均无分。

11．将三个不同的球随机地放入三个不同的盒中，则出现两个空盒的概率为______．


正确答案：

11.1/9

一、单项选择题(本大题共30小题，每小题1分，共30分)

在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。错选、多选或未选均无分。

1.清代由盛转衰的时期是( )

A.乾隆朝后期 B.道光朝后期

C.同治帝时期 D.光绪帝时期


正确答案：A

一、单项选择题(本大题共20小题，每小题1分，共20分)

在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。错选、多选或未选均无分。

1.贯穿《寡人之于国也》始终的论题是( )

A.民何以才能够加多 B.小恩小惠不是王道

C.实行王道的根本措施 D.实行王道的正确态度


正确答案：A
本文阐述了孟子的王道思想和实行王道的根本措施，全文围绕“民不加多”和如何使“民加多”的问题展开论述。

三、名词解释题（本大题共10小题，每小题1分，共10分）

26.邻国之民不加少

加：


正确答案：

答案：加：更。

古典概型事件 名词解释


参考答案：如果某试验可能发生的结果总数是有限的，并且所有结果出现的可能性是相等的，称之为古典概型事件。

原创2021年数学一轮复习精品试题第50讲 古典概型与几何概型第五十讲 古典概型与几何概型班级_ 姓名_ 考号_ 日期_ 得分_ 一、选择题：(本大题共6小题，每小题6分，共36分，将正确答案的代号填在题后的括号内)1一对年轻夫妇和其两岁的孩子做游戏，让孩子把分别写有“One ”，“World ”，“One ”，“Dream ”的四张卡片随机排成一行，若卡片按从左到右的顺序排成“One World One Dream ”，则孩子会得到父母的奖励，那么孩子受到奖励的概率为( )A.112B.113 C.114 D.115解析：试验包含的基本事件的个数为12个，故排对的概率为112，选A.答案：A2在面积为S 的ABC 的边AB 上任取一点，则PBC 的面积大于S4的概率为( )A.14B.12C.34D.23解析：如图，当BM 14BA 时，MBC 的面积为S 4，而当P 在M 、A 之间运动时，PBC的面积大于S 4，而MA 34，则PBC 的面积大于S 4的概率P 34AB 34故选C. 答案：C3有四个游戏盘，将它们水平放稳后，在上面扔一颗小玻璃球，若小球落在阴影部分，则可中奖，小明要想增加中奖机会，应选择的游戏盘是( ) 解析：各选项中奖的概率依次为38，14，13，13，故选A.答案：A4在一个袋子中装有分别标注数字1,2,3,4,5的五个小球，这些小球除标注数字外完全相同，现从中随机取2个小球，则取出的小球标注的数字之和为3或6的概率是( )A.112B.110C.15 D.310解析：随机从袋子中取2个小球的基本事件为(1,2)，(1,3)，(1,4)，(1,5)，(2,3)，(2,4)，(2,5)，(3,4)，(3,5)，(4,5)共有10种，其中数字之和为3或6的有(1,2)，(1,5)，(2,4)，数字之和为3或6的概率是P 310. 答案：D5如图所示，在边长为2的正方形中有一封闭曲线围成的阴影区域在正方形中随机撒一粒豆子，它落在阴影区域内的概率为23，则阴影区域的面积为( ) A.43B.83C.23D.13解析：正方形的面积为4，由S 阴423，知阴影区域的面积为83，选B. 答案：B64张卡片上分别写有数字1,2,3,4，从这4张卡片中随机抽取2张，则取出的2张卡片上的数字之和为奇数的概率为( )A.13B.12 C.23 D.34 解析：从4张卡片中随机取2张共有6种取法，取得2张卡片上数字之和为奇数即1,2，1,4，3,2，3,4四种，故其概率为4623.故选C.答案：C二、填空题：(本大题共4小题，每小题6分，共24分，把正确答案填在题后的横线上) 7甲、乙两人玩数字游戏，先由甲心中任想一个数字记为a ，再由乙猜甲刚才想的数字，把乙想的数字记为b ，且a 、b 1,2,3,4,5,6，若|a b |1，则称“甲乙心有灵犀”，现任意找两个人玩这个游戏，得出他们“心有灵犀”的概率为_解析：数字a ，b 的所有取法有6236种，满足|a b |1的取法有16种，所以其概率为P 163649. 答案：49 8设D 是半径为R 的圆周上的一定点，在圆周上随机取一点C ，连接CD 得一弦，若A 表示“所得弦的长大于圆内接等边三角形的边长”，则P (A )_.解析：如图所示，DPQ 为圆内接正三角形，当C 点位于劣弧 P Q 上时，弦DC PD ，P (A )13 答案：13 9任取一个三位正整数n ，则对数log 2n 是一个正整数的概率是_ 解析：2664,27128,28256,29512,2101024， 满足条件的正整数只有27,28,29三个， 所求的概率是P 39001300. 答案：1300 10已知函数f (x )2ax 2bx 1，若a 是从区间0,2上任取的一个数，b 是从区间0,2上任取的一个数，则此函数在1，)上递增的概率为_解析：令t ax 2bx 1，函数f (x )在1，)上递增，根据复合函数单调性的判断方法，则t ax 2bx 1须在1，)上递增， b2a1，即2a b . 由题意得?0a 2，0b 2，2a b . 画出图示得阴影部分面积 概率为P 2212212234.答案：34 三、解答题：(本大题共3小题，11、12题13分，13题14分，写出证明过程或推演步骤)11汉字是世界上最古老的文字之一，字形结构体现着人类追求均衡对称、和谐稳定的天性如图，三个汉字可以看成是轴对称图形 (1)请再写出2个可看成轴对称图形的汉字；(2)小敏和小慧利用“土”“口”“木”三个汉字设计一个游戏，规则如下：将这三个汉字分别写在背面都相同的三张卡片上，背面朝上，洗匀后抽出一张，放回洗匀后再抽出一张，若两次抽出的汉字能构成上下结构的汉字(如“土”“土”构成“圭”)则小敏获胜，否则小慧获胜你认为这个游戏对谁有利？请用列表或画树状图的方法进行分析，并写出构成的汉字进行说明解：(1)如：田、日等； (2)这个游戏对小慧有利每次游戏时，所有可能出现的如果如下(列表)：总共有9种结果，且每种结果出现的可能性相同，其中能组成上下结构的汉字的结果有4种：(土，土)“圭”，(口，口)“吕”，(木，口)“杏”或“呆”，(口，木)“呆”或“杏”所以小敏获胜的概率为49，小慧获胜的概率为59.所以这个游戏对小慧有利12设有关于x 的一元二次方程x 22ax b 20.(1)若a 是从0,1,2,3四个数中任取的一个数，b 是从0,1,2三个数中任取的一个数，求上述方程有实根的概率；(2)若a 是从区间0,3任取的一个数，b 是从区间0,2任取的一个数，求上述方程有实根的概率解：记事件A 为“方程x 22ax b 20有实根”，当a 0，b 0时，方程x 22ax b 20有实根的充要条件为a b .(1)基本事件共有12个：(0,0)，(0,1)，(0,2)，(1,0)，(1,1)，(1,2)，(2,0)，(2,1)，(2,2)，(3,0)，(3,1)，(3,2)，其中第一个数表示a 的取值，第二个数表示b 的取值事件A 中包含9个基本事件，事件A 发生的概率为 P (A )91234. (2)试验的全部结果所构成的区域为 (a ，b )|0a 3,0b 2 构成事件A 的区域为(a ，b )|0a 3,0b 2，a b ， 所以所求的概率为 P (A )3212223223.13已知集合A x |1x 0，集合B x |ax b 2x 1解：(1)因为a ，b N ，(a ，b )可取(0,1)，(0,2)，(0,3)，(1,1)，(1,2)，(1,3)，(2,1)，(2,2)，(2,3)共9组令函数f (x )ax b 2x 1，x 1,0， 则f (x )a b ln22x.因为a 0,2，b 1,3，所以f (x )0， 即f (x )在1,0上是单调递增函数 f (x )在1,0上的最小值为a b21.要使A B ?，只需a b21所以(a ，b )只能取(0,1)，(1,1)，(1,2)，(1,3)，(2,1)，(2,2)，(2,

请教:2008年10月自考工业用微型计算机真题第1大题第1小题如何解答?

【题目描述】

一、单项选择题（本大题共20小题，每小题2分，共40分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。错选、多选或未选均无分。

1．构成微机系统CPU的两部分是 ( )

 

A．EU和BIU 

B．ALU和BIU

C．ALU和EU 

D．存储器和运算器

 


正确答案：A

请教:2009年7月自考概率论与数理统计(经管类)真题第2大题第1小题如何解答?

【题目描述】

二、填空题(本大题共15小题，每小题2分，共30分)

请在每小题的空格中填上正确答案。错填、不填均无分。

11．将三个不同的球随机地放入三个不同的盒中，则出现两个空盒的概率为______．

 


【参考答案分析】：11.1/9

建立水质预测模型可以概化的条件有:

A:边界条件概化
B:污染源类型
C:水面几何形状
D:含水层性质

答案：A,B,C,D
解析：
题干是依据回忆，信息可能不准不全。所谓的概化，就是为了便于水质预测模型的建立和计算，对相关条件的概括简化，ACD属于水文地质条件的概化，B属于污染源概化。详细见技法书2019版264页，导则书2019版128页.

高中数学《几何概型》
一、考题回顾



答案：
解析：

高中数学《古典概型》
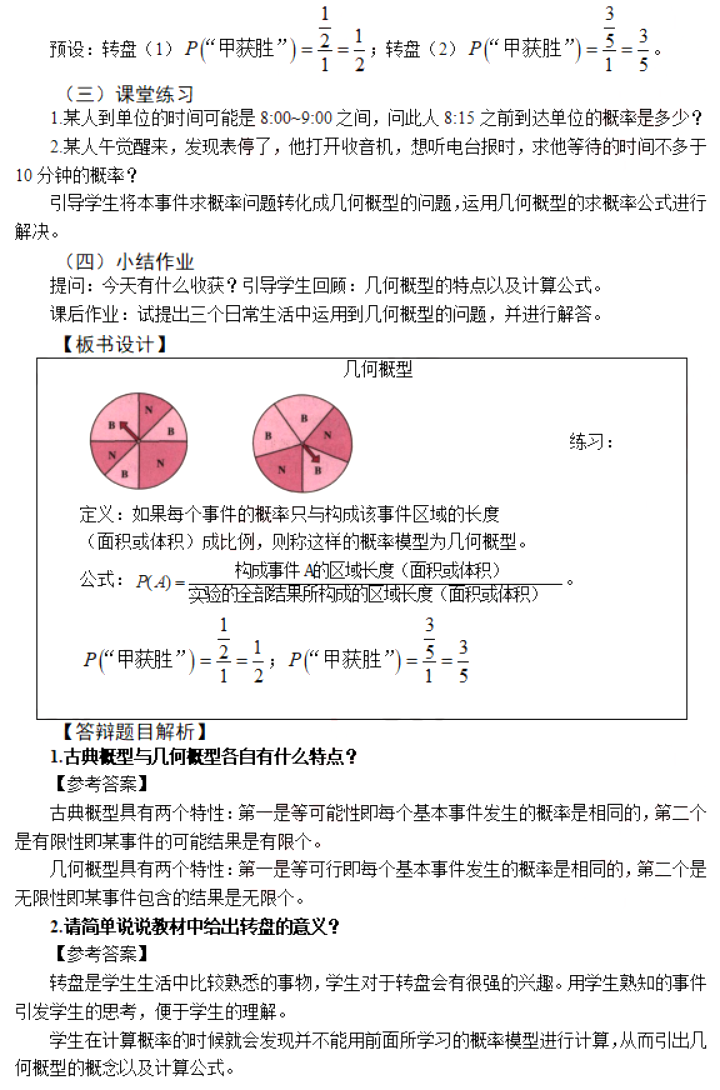
一、考题回顾



二、考题解析
【教学过程】
(一)导入新课
提问：同学们，我们刚刚学习了基本事件的概念，那么什么是基本事件?基本事件又有什么特点呢?有没有人能举一个例子呢?
例1.列举出下列几个随机事件中的基本事件。
1.从a，b，c，d，中任取两个不同的字母的试验。
2.有五根细长的木棒，长度分别为1，3，5，7，9，任取三根。
3.掷两枚硬币，可能出现的结果。
(二)生成概念
提问：这三个例子有什么共同点?
通过学生自主探究，合作交流，师生共同归纳总结共同点，引出古典概型概念：



【答辩题目解析】
1.古典概型与几何概型的异同点?
2.本节课的教学目标是什么?


答案：
解析：
1、区别：古典概型的所有可能出现的基本事件个数为有限个;几何概型的所有可能出现的基本事件个数为无限个。
相同点：(1)每个基本事件出现的可能性一样;
(2)概率公式类似，都是事件所包含的基本事件的个数比上基本事件的总个数。

2、会判断古典概型，会用列举法计算一些随机事件所含的基本事件数和试验中基本事件的总数;能够利用概率公式求解一些简单的古典概型的概率。
【过程与方法】
通过从实际问题中抽象出数学模型的过程，提升从具体到抽象从特殊到一般的分析问题的能力。
【情感态度与价值观】
增加学生合作学习交流的机会，在体会概率意义的同时，感受与他人合作的重要性以及初步形成实事求是地科学态度和锲而不舍的求学精神。

更多 “[原创]2021年数学一轮复习精品试题第50讲 古典概型与几何概型” 相关考题
考题 《普通高中数学课程标准（实验）》关于“古典概型”的教学要求是：“古典概型的教学应让学生通过实例理解古典概型的特征：实验结果的有限性和每一个实验结果出现的等可能性，让学生初步学会把一些实际问题化为古典概型，教学中不要把重点放在‘如何计算’上”。 请完成下列任务： （1）结合上述教学要求，请设计高中“古典概型”起始课的教学目标；（6分） （2）请设计两个符合古典概型的正例，以及两个不符合古典概型的反例，以便理解古典概型的特征；（12分） （3）抛掷一枚质地均匀的骰子（六个面分别有1、2、3、4、5、6个点），请用两种不同解法求出现偶数点的概率，并说明采用两种解法对帮助学生理解古典概型的作用。（12分）答案：解析：本题主要以 “古典概型”为例，考查古典概型概率的基础知识、高中数学课程概述、教学设计工作的基本环节、常用的教学方法、课堂导入技巧及教学设计工作等相关知识，比较综合性地考查学科知识、课程知识、教学知识以及教学技能的基本知识和基本技能。 （1）新课标倡导三维教学目标，知识与技能目标、过程与方法目标、情感态度与价值观目标。知识与技能目标，是对学生学习结果的描述，即学生同学习所要达到的结果，又叫结果性目标。这种目标一般有三个层次的要求：学懂、学会、能应用。 过程与方法目标，是学生在教师的指导下，如何获取知识和技能的程序和具体做法，是过程中的目标，又叫程序性目标。这种目标强调三个过程：做中学、学中做、反思。 情感态度与价值观目标，是学生对过程或结果的体验后的倾向和感受，是对学习过程和结果的主观经验，又叫体验性目标。它的层次有认同、体会、内化三个层次。 知识与技能目标是过程与方法目标、情感态度与价值观目标的基础；过程与方法目标是实现知识与技能目标的载体，情感态度与价值观目标对其他目标有重要的促进和优化作用。 （2）古典概型概念：①试验中所有可能出现的事件只有有限个；②每个基本事件出现的可能性相等。只有同时具有这两个特点的概率模型，称为古典概率概型。举例子时针对古典概型中的两种特性举出即可。 （3）采用两种不同解法求出现偶数点的概率，如公式法、枚举法等，并说明采用两种解法对帮助学生理解古典概型的作用。
查看答案
考题 《普通高中数学课程标准（实验）》关于“古典概型”的教学要求是：“古典概型的教学应让学生通过实例理解古典概型的特征：实验结果的有限性和每一个实验结果出现的等可能性，让学生初步学会把一些实际问题化为古典概型，教学中不要把重点放在‘如何计算’上”。 请完成下列任务： （1）结合上述教学要求，请设计高中“古典概型”起始课的教学目标；（6分） （2）请设计两个符合古典概型的正例，以及两个不符合古典概型的反例，以便理解古典概型的特征；（12分） （3）抛掷一枚质地均匀的骰子（六个面分别有1、2、3、4、5、6个点），请用两种不同解法求出现偶数点的概率，并说明采用两种解法对帮助学生理解古典概型的作用。（12分）答案：解析：本题主要以 “古典概型”为例，考查古典概型概率的基础知识、高中数学课程概述、教学设计工作的基本环节、常用的教学方法、课堂导入技巧及教学设计工作等相关知识，比较综合性地考查学科知识、课程知识、教学知识以及教学技能的基本知识和基本技能。 （1）新课标倡导三维教学目标，知识与技能目标、过程与方法目标、情感态度与价值观目标。知识与技能目标，是对学生学习结果的描述，即学生同学习所要达到的结果，又叫结果性目标。这种目标一般有三个层次的要求：学懂、学会、能应用。 过程与方法目标，是学生在教师的指导下，如何获取知识和技能的程序和具体做法，是过程中的目标，又叫程序性目标。这种目标强调三个过程：做中学、学中做、反思。 情感态度与价值观目标，是学生对过程或结果的体验后的倾向和感受，是对学习过程和结果的主观经验，又叫体验性目标。它的层次有认同、体会、内化三个层次。 知识与技能目标是过程与方法目标、情感态度与价值观目标的基础；过程与方法目标是实现知识与技能目标的载体，情感态度与价值观目标对其他目标有重要的促进和优化作用。 （2）古典概型概念：①试验中所有可能出现的事件只有有限个；②每个基本事件出现的可能性相等。只有同时具有这两个特点的概率模型，称为古典概率概型。举例子时针对古典概型中的两种特性举出即可。 （3）采用两种不同解法求出现偶数点的概率，如公式法、枚举法等，并说明采用两种解法对帮助学生理解古典概型的作用。
查看答案
考题 问答题结合实例谈谈，在高中课程教学中，为什么不强调几何概型，而强调随机模拟的思想？正确答案： 在高中课程的教学中，应对模拟的思想给予特别的关注，这个思想十分重要。典型的例子是用几何概率来计算平面图形的面积，它很直观地给出了随机模拟的思想。但教师应该清楚，随机模拟应用的范围十分广泛，绝不仅仅限于计算几何图形的面积或体积。事实上，许多不能用数学公式描述的问题，都可以通过模拟来实现。例如，可以让学生在超市收银台前，记录每分钟到达的人数，从而得到到达0个人的概率、到达1个人的概率……，再记录为每个人服务的时间，得到服务时间不足1分钟的概率、服务时间不足2分钟的概率……然后，可以通过模拟，再现收银台前顾客来到的状况。把一个实际问题转化为一个可以模拟的问题是一个非常重要的意识，对于学生以后走向社会是一个重要的本领。在解决实际问题时，通常是用离散的量模拟连续变化的量，这些思想都很重要。几何概型讨论的是连续随机变量中的均匀分布，历史上它的解最早是几何方法来求得。由于积分的出现，这种方法目前意义已经不大。因此，不应该是我们的重点。我们只用它来介绍随机模拟。事实上，在教学中还可以选择不同的工具进行随机模拟，例如随机数表、计算器等等。 解析： 暂无解析
查看答案
考题 通信建设工程概、预算文件由编制说明和概、预算表组成。其中的概、预算表格统一使用（）。A、五种共五张表格B、五种共六张表格C、五种共七张表格D、五种共八张表格正确答案:D
查看答案
考题 单选题通信建设工程概、预算文件由编制说明和概、预算表组成。其中的概、预算表格统一使用（）。A 五种共五张表格B 五种共六张表格C 五种共七张表格D 五种共八张表格正确答案： B 解析： 暂无解析
查看答案
考题 结合实例谈谈，在高中课程教学中，为什么不强调几何概型，而强调随机模拟的思想？正确答案: 在高中课程的教学中，应对模拟的思想给予特别的关注，这个思想十分重要。典型的例子是用几何概率来计算平面图形的面积，它很直观地给出了随机模拟的思想。但教师应该清楚，随机模拟应用的范围十分广泛，绝不仅仅限于计算几何图形的面积或体积。事实上，许多不能用数学公式描述的问题，都可以通过模拟来实现。例如，可以让学生在超市收银台前，记录每分钟到达的人数，从而得到到达0个人的概率、到达1个人的概率……，再记录为每个人服务的时间，得到服务时间不足1分钟的概率、服务时间不足2分钟的概率……然后，可以通过模拟，再现收银台前顾客来到的状况。把一个实际问题转化为一个可以模拟的问题是一个非常重要的意识，对于学生以后走向社会是一个重要的本领。在解决实际问题时，通常是用离散的量模拟连续变化的量，这些思想都很重要。几何概型讨论的是连续随机变量中的均匀分布，历史上它的解最早是几何方法来求得。由于积分的出现，这种方法目前意义已经不大。因此，不应该是我们的重点。我们只用它来介绍随机模拟。事实上，在教学中还可以选择不同的工具进行随机模拟，例如随机数表、计算器等等。
查看答案
考题 《普通高中数学课程标准（实验）》关于“古典概型”的教学要求是：“古典概型的教学应让学生通过实例理解古典概型的特征：实验结果的有限性和每一个实验结果出现的等可能性，让学生初步学会把一些实际问题化为古典概型，教学中不要把重点放在‘如何计算’上”。 请完成下列任务： （1）结合上述教学要求，请设计高中“古典概型”起始课的教学目标；（6分） （2）请设计两个符合古典概型的正例，以及两个不符合古典概型的反例，以便理解古典概型的特征；（12分） （3）抛掷一枚质地均匀的骰子（六个面分别有1、2、3、4、5、6个点），请用两种不同解法求出现偶数点的概率，并说明采用两种解法对帮助学生理解古典概型的作用。（12分）答案：解析：本题主要以 “古典概型”为例，考查古典概型概率的基础知识、高中数学课程概述、教学设计工作的基本环节、常用的教学方法、课堂导入技巧及教学设计工作等相关知识，比较综合性地考查学科知识、课程知识、教学知识以及教学技能的基本知识和基本技能。 （1）新课标倡导三维教学目标，知识与技能目标、过程与方法目标、情感态度与价值观目标。知识与技能目标，是对学生学习结果的描述，即学生同学习所要达到的结果，又叫结果性目标。这种目标一般有三个层次的要求：学懂、学会、能应用。 过程与方法目标，是学生在教师的指导下，如何获取知识和技能的程序和具体做法，是过程中的目标，又叫程序性目标。这种目标强调三个过程：做中学、学中做、反思。 情感态度与价值观目标，是学生对过程或结果的体验后的倾向和感受，是对学习过程和结果的主观经验，又叫体验性目标。它的层次有认同、体会、内化三个层次。 知识与技能目标是过程与方法目标、情感态度与价值观目标的基础；过程与方法目标是实现知识与技能目标的载体，情感态度与价值观目标对其他目标有重要的促进和优化作用。 （2）古典概型概念：①试验中所有可能出现的事件只有有限个；②每个基本事件出现的可能性相等。只有同时具有这两个特点的概率模型，称为古典概率概型。举例子时针对古典概型中的两种特性举出即可。 （3）采用两种不同解法求出现偶数点的概率，如公式法、枚举法等，并说明采用两种解法对帮助学生理解古典概型的作用。
查看答案
考题 问答题结合实例谈谈，在高中课程教学中，为什么不强调几何概型，而强调随机模拟的思想？正确答案： 在高中课程的教学中，应对模拟的思想给予特别的关注，这个思想十分重要。典型的例子是用几何概率来计算平面图形的面积，它很直观地给出了随机模拟的思想。但教师应该清楚，随机模拟应用的范围十分广泛，绝不仅仅限于计算几何图形的面积或体积。事实上，许多不能用数学公式描述的问题，都可以通过模拟来实现。例如，可以让学生在超市收银台前，记录每分钟到达的人数，从而得到到达0个人的概率、到达1个人的概率……，再记录为每个人服务的时间，得到服务时间不足1分钟的概率、服务时间不足2分钟的概率……然后，可以通过模拟，再现收银台前顾客来到的状况。把一个实际问题转化为一个可以模拟的问题是一个非常重要的意识，对于学生以后走向社会是一个重要的本领。在解决实际问题时，通常是用离散的量模拟连续变化的量，这些思想都很重要。几何概型讨论的是连续随机变量中的均匀分布，历史上它的解最早是几何方法来求得。由于积分的出现，这种方法目前意义已经不大。因此，不应该是我们的重点。我们只用它来介绍随机模拟。事实上，在教学中还可以选择不同的工具进行随机模拟，例如随机数表、计算器等等。 解析： 暂无解析
查看答案
考题 高中数学《古典概型》 一、考题回顾 二、考题解析 【教学过程】 (一)导入新课 提问：同学们，我们刚刚学习了基本事件的概念，那么什么是基本事件?基本事件又有什么特点呢?有没有人能举一个例子呢? 例1.列举出下列几个随机事件中的基本事件。 1.从a，b，c，d，中任取两个不同的字母的试验。 2.有五根细长的木棒，长度分别为1，3，5，7，9，任取三根。 3.掷两枚硬币，可能出现的结果。 (二)生成概念 提问：这三个例子有什么共同点? 通过学生自主探究，合作交流，师生共同归纳总结共同点，引出古典概型概念： (1)试验中所有可能出现的基本事件只有有限个;(有限性) 1.古典概型与几何概型的异同点? 2.本节课的教学目标是什么?答案：解析：1 区别：古典概型的所有可能出现的基本事件个数为有限个;几何概型的所有可能出现的基本事件个数为无限个。 相同点：(1)每个基本事件出现的可能性一样; (2)概率公式类似，都是事件所包含的基本事件的个数比上基本事件的总个数。 2. 【知识与技能】 会判断古典概型，会用列举法计算一些随机事件所含的基本事件数和试验中基本事件的总数;能够利用概率公式求解一些简单的古典概型的概率。 【过程与方法】 通过从实际问题中抽象出数学模型的过程，提升从具体到抽象从特殊到一般的分析问题的能力。 【情感态度与价值观】 增加学生合作学习交流的机会，在体会概率意义的同时，感受与他人合作的重要性以及初步形成实事求是地科学态度和锲而不舍的求学精神。
查看答案
考题 《普通高中数学课程标准（实验）》关于“古典概型”的教学要求是：“古典概型的教学应让学生通过实例理解古典概型的特征：实验结果的有限性和每一个实验结果出现的等可能性，让学生初步学会把一些实际问题化为古典概型，教学中不要把重点放在‘如何计算’上”。 请完成下列任务： （1）结合上述教学要求，请设计高中“古典概型”起始课的教学目标；（6分） （2）请设计两个符合古典概型的正例，以及两个不符合古典概型的反例，以便理解古典概型的特征；（12分） （3）抛掷一枚质地均匀的骰子（六个面分别有1、2、3、4、5、6个点），请用两种不同解法求出现偶数点的概率，并说明采用两种解法对帮助学生理解古典概型的作用。（12分）答案：解析：本题主要以 “古典概型”为例，考查古典概型概率的基础知识、高中数学课程概述、教学设计工作的基本环节、常用的教学方法、课堂导入技巧及教学设计工作等相关知识，比较综合性地考查学科知识、课程知识、教学知识以及教学技能的基本知识和基本技能。 （1）新课标倡导三维教学目标，知识与技能目标、过程与方法目标、情感态度与价值观目标。知识与技能目标，是对学生学习结果的描述，即学生同学习所要达到的结果，又叫结果性目标。这种目标一般有三个层次的要求：学懂、学会、能应用。 过程与方法目标，是学生在教师的指导下，如何获取知识和技能的程序和具体做法，是过程中的目标，又叫程序性目标。这种目标强调三个过程：做中学、学中做、反思。 情感态度与价值观目标，是学生对过程或结果的体验后的倾向和感受，是对学习过程和结果的主观经验，又叫体验性目标。它的层次有认同、体会、内化三个层次。 知识与技能目标是过程与方法目标、情感态度与价值观目标的基础；过程与方法目标是实现知识与技能目标的载体，情感态度与价值观目标对其他目标有重要的促进和优化作用。 （2）古典概型概念：①试验中所有可能出现的事件只有有限个；②每个基本事件出现的可能性相等。只有同时具有这两个特点的概率模型，称为古典概率概型。举例子时针对古典概型中的两种特性举出即可。 （3）采用两种不同解法求出现偶数点的概率，如公式法、枚举法等，并说明采用两种解法对帮助学生理解古典概型的作用。
查看答案
热门标签
最新考题
最新试卷
热门试卷