八年级上学期第二章一次函数单元检测题

网友您好，请在下方输入框内输入要搜索的题目：

八年级上学期第二章一次函数单元检测题

函数Int(Rnd*6+1)的取值范围是（）。

A．从1到7共7个整数

B．从0到7共8个整数

C．从1到6共6个整数

D．从0到6共7个整数

正确答案：C

正比例函数ｙ＝ｘ的图像与反比例函数y=k/x图像有一个交点的纵坐标是２，求（１）当ｘ＝－３时，反比例函数ｙ的值；（２）当-3<x<-1时反比例函数ｙ的取值范围？

函数Int(Rnd*6+1)的取值范围是

A．1～7共7个整数

B．0～7共8个整数

C．1～6共6个整数

D．0～6共7个整数

正确答案：C
解析：Rnd函数产生的是大于等于0而小于1的随机数字，因此Rnd*6+1产生的数值范围是大于等于1而小于7，因此用Int函数取整后的结果范围应该是1～6共6个整数。

请教:2012年初中数学《函数及其图象》测验卷第1大题第1小题如何解答?

【题目描述】

函数y=的自变量的取值范围是( )

A、x>0且x≠0

B、x≥0且x≠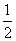

C、x≥0

D、x≠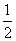

正确答案：B

在函数y=[√(x-6)]/(x-8)中，自变量x的取值范围是

A.x＞6

B.x≥6

C.x＞8

D.x≥6且x≠8

正确答案：D

八年级上学期第二章一次函数单元检测题班级_ 姓名_一、填空题（本题共10小题，每题3分，共30分） AUTONUM 在球的体积公式中,常量是_，变量是_，的取值范围是_ AUTONUM 若是正比例函数，则 AUTONUM 函数的自变量的取值范围是_ AUTONUM 函数经过点，则，当时，当时， AUTONUM 直线与轴的交点坐标是_，与轴的交点坐标是_，且随的增大而_ AUTONUM 一条直线与直线平行，且与轴交于点，则这条直线的解析式为_ AUTONUM 我校举行田径运动会，如图是小亮参加百米赛跑时所跑路程（米）与时间（秒）的图象，则与的函数关系式为_，自变量的取值范围是_ AUTONUM 把直线向下平移3个单位，得到的直线的解析式为_ AUTONUM 如图，已知两直线与交于点P，则关于的二元一次方程组的解是_ AUTONUM 已知一次函数，当时，则二、选择题（本题共10小题，每题3分，共30分） AUTONUM 下列各点中，不在直线上的点是（） A B C D AUTONUM 下列函数中，不是关于的一次函数的是（） A B C D AUTONUM 对于直线，下列说法中错误的是（） A随的增大而减小 B与直线平行 C与轴的交点坐标是 D与直线交于点 AUTONUM 小明根据邻居家的故事写了一首诗：“儿子学成今日返，老父早早到车站，儿子到后细端详，父子高兴把家还。如果用纵轴表示父亲与儿子行进中离家的距离，用横轴表示父亲离家的时间，那么下面的图象与上述诗的含义大致吻合的是（） AUTONUM 已知点都在直线上，的大小关系是（） A B C D无法确定 AUTONUM 若一次函数与正比例函数相交于点，则一次函数的解析式为（） A B C D AUTONUM 已知一次函数的图象如图所示，则的符号是（） A B C D AUTONUM 已知两条直线与交于点，且，当时，的取值范围是（） A B C D AUTONUM 已知直线与直线的交点在第四象限，则的符号是（） A B C D AUTONUM 若一次函数的图象不经过第三象限，则下列结论成立的是（） A B C D三、解答题（本大题共40分） AUTONUM （本题满分6分）已知一次函数的图象经过点和，求这个函数的解析式；画出这个函数的图象；若函数图象与轴交于点A，与轴交于点B，求OAB的面积。 AUTONUM （本题满分6分）已知与成正比例，且时，求与的函数关系式；若，求的值；若，求的值。 AUTONUM （本题满分6分）甲、乙两人同时从自己家出发，赶往学校，如图所示，表示他们出发的时间，表示他们离甲的家的距离，根据甲、乙两人行进的图象，回答下列问题：甲、乙两家相距_千米；当时，乙在甲的前面，当时，甲在乙的前面。甲、乙两人在第_分钟距甲的家_千米处相遇。若甲、乙两人保持速度不变，先到达学校的是_ AUTONUM (本题满分6分)有一个水箱，它的容积为500升，水箱内原有水200升，现要将水箱注满，已知每分钟注水10升（注满就停止注水）写出水箱内的水量Q（升）与时间的函数关系式，并求自变量的取值范围。画出这个函数的图象。 AUTONUM （本题满分8分）如图，已知两点的坐标为求点A关于轴的对称点的坐标；求直线的解析式，并画出直线；求的面积S。 AUTONUM （本题满分8分）某公司销售产品A，第一批产品A上市30天全部售完，日销售量（件）与上市时间（天）之间的函数关系如图所示，求与的函数关系式；求这批产品A的总件数。参考答案：一、填空题：1、；2、3、4、5、；增大6、7、8、9、10、3或1二、选择题：11、C 12、B 13、C 14、B 15、A 16、B 17、B 18、A 19、C 20、C三、解答题：21、解：设一次函数的解析式为：，由于图象经过点和，解之得：一次函数的解析式为：略由，可知22、解：设，由时，解得：与的函数关系式为：当时，则当时，则23、 1千米； 20分钟；2千米甲24、解：略25、解：A点关于轴对称点的坐标为设的解析式为：，则题意得：，解之得：的解析式为：26、解：S= = =这批产品A的总件数为1056件。

已知二次函数y1=x2-x-2和一次函数y2=x+1的两个交点分别为A(-1，0)，B(3，4)，当y1＞y2时，自变量x的取值范围是（）

A．x＜-1或x＞3 B．-1＜x＜3 C．x＜-1 D．x＞3

正确答案：A

函数(x)=x2+2(m-1)x+2在区间(-∞，4)上是减函数，则实数m的取值范围是( )

A.m≥-3
B.m=-3
C.m≤-3
D.m≥3

答案：C

解析：

【考情点拨】本题主要考查的知识点为减函数的性质．【应试指导】由已知条件(x)=x2+2(m-1)x+2(x)=(x+m-1)2-(m-1)2+2，故(x)的对称轴为x=1-m，又∵(x)在(-∞，4)上是减函数，∴1-m≥4，即m≤-3．

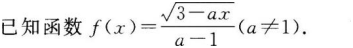
(1)若a>0，则?(x)的定义域是__________；
(2)若?(x)在区间(0，1]上是减函数，则实数a的取值范围是__________．

答案：

解析：

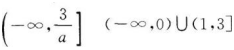
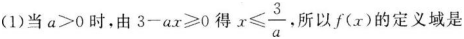
判定系数的意义是（）。

A在因变量取值的总离差中可以由自变量取值所解释的比例

B它反映了自变量对因变量取值的决定程度

C当取值等于1时，拟合是完全的，所有观测值都落在回归直线上

D当取值等于0时，自变量的取值与因变量无关

E取值越接近1，表明回归直线的拟合越好；相反，取值越接近0；回归直线的拟合越差

A,B,C,D,E
略

函数y=x²-2ax+1，若它的增区间是[2，+∞），则a的取值是多少？若它在区间[2，+∞）上递增，则a的取值范围是什么？

正确答案: a=2；a≤2。

网友您好， 请在下方输入框内输入要搜索的题目：

更多 “八年级上学期第二章一次函数单元检测题” 相关考题

网友您好，请在下方输入框内输入要搜索的题目：