网友您好， 请在下方输入框内输入要搜索的题目：
若反比例函数的图象经过点A(-2,1) ,则它的表达式是 _________________ ．
作出函数y=3-2x的图象，根据图象回答下列问题：
（1）y的值随着x值增大而__________;
（2）图象与x轴的交点坐标是_________________，
与y轴的交点坐标是_______________；
（3）当x__________时，y＞0 。
在同一直角坐标系内一次作出函数y=x+1，y=2x+1，y=3x+1的图象。
（1）这几个图象之间有什么差别，又有什么联系？
（2）一次函数y=kx+b的一次项系数k对函数的图象有什么影响？
（1）这几个图像都经过（0,1）点，且y都随x的增大而增大，但是这几个图像的倾斜程度不同。
（2）对图像倾斜度有影响！
已知函数 y=x²-4x+3。
（1）画出函数的图象；
（2）观察图象，当x取哪些值时，函数值为0？
画出函数 y=x²-2x-3的图象，利用图象回答：
（1）方程 x²-2x-3=0 的解是什么；
（2）x取什么值时，函数值大于0 ；
（3）x取什么值时，函数值小于0 。
摘要:2.4.1二次函数的图象(本栏目内容，在学生用书中以活页形式分册装订！)一、选择题(每小题5分，共20分)1.二次函数y＝ax2＋bx＋c的图象如图所示，则点(a，c)在…………………………………()A.第一象限B.第二象限C.第三象限D.第四象限【答案】D2.如何平移抛物线y＝2x2可得到抛物线y＝2(x－4)2－1…………………………()A.向左平移4个单位，再向上平移1个单位B.向左平移4个单位，再向下平移1个单位C.向右平移4个单位，再向上平移1个单位D.向右平移4个单位，再向下平移1个单位【解析】要得到y＝2(x－4)2－1的图象，只需将y＝2x2的图象向右平移4个单位，再向下平移1个单位.【答案】D3.已知抛物线与x轴交于点(－1,0)，(1,0)，并且与y轴交于点(0,1)，则抛物线的解析式为…………………………………()A.y＝－x2＋1B.y＝x2＋1C.y＝－x2－1D.y＝x2－1【解析】由题意抛物线对称轴是y轴且开口向下，顶点(0,1)，故抛物线为y＝－x2＋1.【答案】A4.二次函数y＝x2＋ax＋b，若a＋b＝0，则它的图象必经过点…………()A.(－1，－1)B.(1，－1)C.(1,1)D.(－1,1)【解析】∵a＋b＝0，∴当x＝1时，y＝1＋a＋b＝1，∴过点(1,1).【答案】C二、填空题(每小题5分，共10分)5.函数y＝x2＋(a＋2)x＋3(a≤x≤b)的图象关于直线x＝1对称，则b＝. 【解析】对称轴x＝－＝1，∴a＝－4.又a、
【题目描述】
如果点P（－1,b）在直线y=2x+3上，那么点P到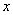
轴的距离为__________.
【参考答案分析】：
1
11 、点 A （ 2 ， y 1 ） 、 B （ 3 ， y 2 ）是二次函数 y=x 2- 2x+1 的图象上两点，则 y 1 与 y 2 的大小关
系为 y 1 _________ y 2 （填 “ ＞ ” 、 “ ＜ ” 、 “ = ” ） ．
<
考点：二次函数图象上点的坐标特征。
分析：本题需先根据已知条件求出二次函数的图象的对称轴，再根据点A、B的横坐标的大小即可判断出y1与y2的大小关系．
解答：解：∵二次函数y=x2﹣2x+1的图象的对称轴是x=1，
在对称轴的右面y随x的增大而增大，
∵点A（2，y1）、B（3，y2）是二次函数y=x2﹣2x+1的图象上两点，
23，
∴y1y2．
故答案为：．
点评：本题主要考查了二次函数图象上点的坐标特征，在解题时要能灵活应用二次函数的图象和性质以及点的坐标特征是本题的关键．
已知m是整数，且一次函数y=(m+4)x+m+2的图象不过第二象限，则m= ；
－3或－2
已知一次函数的图象经过点A（2，1），B（－1，－3）
（1）求此一次函数的解析式；
（2）求此一次函数的图象与x轴、y轴的交点坐标；
（3）求此一次函数的图象与两坐标轴所围成的三角形面积。
（1）y=
x － 
(2)与x轴的交点坐标（
,0）；与y轴的交点坐标(0,－ 
)
(3)面积为
B.函数f(x)在定义域范围内，y随着x的增大而减小
C.若点C(-1，m)，点B(2，n)，在函数f(x)的图象上，则m＜n
D.函数f(x)图象对称轴的直线方程是y=x
m＜n，C正确；函数f(x)图象对称轴有两条，y=x和y=-x，D错误。
更多 “《二次函数性质的再研究》二次函数的图象同步测试题北师大版” 相关考题
- 肝性脑病患者口服新霉素为（）A、减少肠道氨的生成B、减少肠道氨的吸收C、促进肠道氨的代谢D、减少假神经递质的形成E、促进锰的代谢
- 单选题下列那项是低应变法不能反映的（）A 桩身缺陷位置B 桩身缺陷程度C 桩身混凝土强度D 桩身混凝土传播速度
- 男，45岁，因骨盆骨折住院。X线检查发现多部位溶骨性病变。实验室检查：骨髓浆细胞占25％，血沉50mm／h，血红蛋白为80g／L，尿本周蛋白阳性，血清蛋白电泳呈现M蛋白，血清免疫球蛋白含量IgG8g／L、IgA12g／L、IgM0.2g／L。如进一步对该患者进行分型应为（）A、IgG型B、IgA型C、IgD型D、IgE型E、非分泌型
- 下列门控心血池显像测定中，最常用的反映心脏整体功能的指标是（）。A、PERB、PFRC、LVEFD、TPFRE、RWM
- 多选题成桩质量评价，不宜判定受检桩类别分类（）A优良、合格、不合格B满足设计要求、不满足设计要求CⅠ类、Ⅱ类、Ⅲ类、Ⅳ类桩D完整桩、非完整桩
- 判断题钻芯法检测应根据混凝土设计强度等级选用合适的合金钻头。A 对B 错
- 填空题为设计提供依据的抗拔试验，如发现灌注桩桩身中下部有明显的（）时，不宜作为抗拔试验桩。
- 可以排除肺血栓栓塞症的检查是A、肺通气／灌注断层显像示通气／灌注不匹配，其范围不少于一个肺段或两个亚肺段B、肺通气／灌注断层显像示通气／灌注匹配或反向不匹配C、肺通气显像异常D、下肢静脉显像出现放射性充盈缺损或侧支循环E、肺通气显像正常
- 下列哪种显像剂用于诊断慢性炎症效果最佳（）A、99mTc-MDPB、67Ga-枸橼酸镓C、99mTc-WBCD、99mTc-IgGE、In-WBC
- 上述何种检查可以确诊DVTA、肺通气／灌注断层显像示通气／灌注不匹配，其范围不少于一个肺段或两个亚肺段B、肺通气／灌注断层显像示通气／灌注匹配或反向不匹配C、肺通气显像异常D、下肢静脉显像出现放射性充盈缺损或侧支循环E、肺通气显像正常