网友您好, 请在下方输入框内输入要搜索的题目:
在同一直角坐标系内一次作出函数y=x+1,y=2x+1,y=3x+1的图象。
(1)这几个图象之间有什么差别,又有什么联系?
(2)一次函数y=kx+b的一次项系数k对函数的图象有什么影响?
(1)这几个图像都经过(0,1)点,且y都随x的增大而增大,但是这几个图像的倾斜程度不同。
(2)对图像倾斜度有影响!
已知函数 y=x²-4x+3。
(1)画出函数的图象;
(2)观察图象,当x取哪些值时,函数值为0?
已知函数f(x)=a2+k的图象经过点(1,7),且其反函数f-1(x)的图像经过点(4,0),则函数f(x)的表达式是 ( )
A.f(x)=4x+3
B.f(x)=2x+5
C.f(x)=5x+2
D.f(x)=3x+5
已知m是整数,且一次函数y=(m+4)x+m+2的图象不过第二象限,则m= ;
-3或-2
已知一次函数的图象经过点A(2,1),B(-1,-3)
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积。
(1)y=![]() x -
x - ![]()
(2)与x轴的交点坐标(![]() ,0);与y轴的交点坐标(0,-
,0);与y轴的交点坐标(0,- ![]() )
)
(3)面积为![]()
一次函数单元检测 B 眼识金!1已知函数 y=kx+b 的图象如图,则 y=2kx+b 的图象可能是()、 、 、 、2已知一次函数 y=(x+k+1 的图象不过第三象限,则 k 的取值范围是()、k 2、k 2、- 1 k 2、- 1 k 23如图,直线 y=kx+b 交坐标轴于 A,B 两点,则不等式 kx+b0 的解集是()、x 、x 3、x 、x 34已知直线的方程式为 ax+by+c=0,且 a0cb,则方程式的图象为()、 、 、 、5在平面直角坐标系内,直线 y= x+3 与两坐标轴交于 A、B 两点,点 O 为坐标原点,若在该坐标平面内有以点34P(不与点 A、B、O 重合)为顶点的直角三角形与 等,且这个以点 P 为顶点的直角三角形与 一条公共边,则所有符合条件的 P 点个数为()、9 个 、7 个 、5 个 、3 个6如图,点 A 的坐标为(),点 B 在直线 y=x 上运动,当线段 短时,点 B 的坐标为()、( 0, 0) 、 、 、2-( , ) 1, ) 2-( , )7根据生物学研究结果,青春期男女生身高增长速度呈现如下图规律,由图可以判断,下列说法错误的是()、男 生 在 13 岁 时 身 高 增 长 速 度 最 快 、女 生 在 10 岁 以 后 身 高 增 长 速 度 放 慢 、1 1 岁 时 男 女 生 身 高 增 长 速 度 基 本 相 同 、女 生 身 高 增 长 的 速 度 总 比 男 生 慢8汽车开始行驶时,油箱内有油 40 升,如果每小时耗油 5 升,则油箱内余油量 Q(升)与行驶时间 t(时)的函数关系用图象表示应为()、 、 、 、9已知一次函数的图象与直线 y= 平行,且过点(8,2),那么此一次函数的解析式为()、y =、y =-x

B.函数f(x)在定义域范围内,y随着x的增大而减小
C.若点C(-1,m),点B(2,n),在函数f(x)的图象上,则m<n
D.函数f(x)图象对称轴的直线方程是y=x

m<n,C正确;函数f(x)图象对称轴有两条,y=x和y=-x,D错误。
(1)求k的取值范围;
(2)若|x1-x2|=x1x2-1,求k的值。
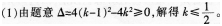
(2)由方程有x1+x2=2(k-1),x1x2=k2。若x1-x2=x1x2-1,贝4(x1+x2)2-4x1x2=x1x2-1)2,即4(k-1)2-4k2=(k2-1)2,即(k2-2k+3)(k2+2k-1)=0,解得
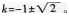
(1)求出图象与戈轴的交点A,B的坐标;
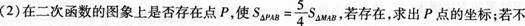
存在,请说明理由;
° (3)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.

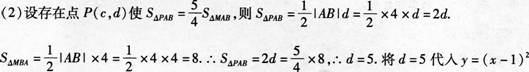
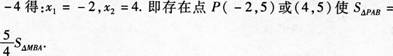
(3)如图,当直线Y=x+b经过A(-1,0)时-1+b=0,
可得b=1,又因为b<1,
故可知Y=x+b在Y=x+1的下方,
当直线Y=x+b经过点B(3,0)时,3+b=0,则b=-3,
由图可知,b的取值范围为-3<b<1时,
直线Y=x+b(b<1)与此图象有两个公共点.

B.-1.5V
C.-0.5V
D.0.5V

B.Au=6.5,ri=5.2Ω,ro=20kΩ
C.Au=-65,ri=1kΩ,ro=6kΩ
D.Au=65,ri=200Ω,ro=2kΩ
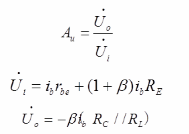
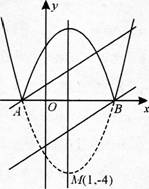
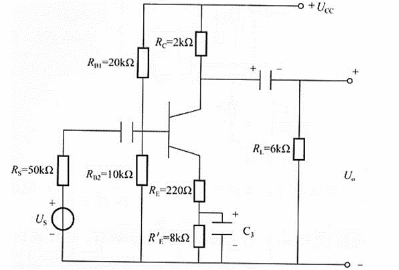
故晶体管的放大倍数
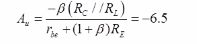
输入电阻ri=RB1//RB2//[rbe+(1+β)RE]=20//10//23.22≈5.18kΩ。
输出电阻ro≈RC=2kΩ。

更多 “2014年最新人教版八年级下一次函数单元检测B卷(带详细答案)” 相关考题
- 问答题试判断以下各式是否为重言式。 (1)(P→Q)→(Q→P) (2)P→(P→Q) (3)Q→(P→Q) (4)(P∧Q)→(P→Q) (5)((P→Q)∨(R→Q))→((P∨R)→Q) (6)((P→Q)∨((R→S))→((P∨R)→(Q∨S))
- 在等容收缩期,心脏各瓣膜的功能状态是()。A、房室瓣关闭,半月瓣开放B、房室瓣开放,半月瓣关闭C、房室瓣关闭,半月瓣关闭D、房室瓣开放,半月瓣开放E、二尖瓣关闭,三尖瓣开放
- 单选题设谓词P(x):x是奇数,Q(x):x是偶数,谓词公式∃x(P(x)∨Q(x))在哪个个体域中为真?( )A 自然数B 实数C 复数D A,B,C均成立
- 单选题设f是由群到群的同态映射,则Ker(f)是( )。A G`的子群B G的子群C 包含G`D 包含G
- 下列哪种细菌感染一般不侵入血流()。A、伤寒杆菌B、葡萄球菌C、脑膜炎球菌D、淋球菌E、链球菌
- 关于朊病毒蛋白描述错误的是()。A、病毒蛋白致病前后一级结构完全一致B、病毒蛋白致病前后二级结构不同C、朊病毒是由外源基因编码的D、朊病毒以蛋白为模板进行转化E、抗核酸药物对朊病毒无效
- 人血浆内蛋白质总浓度大约为()。A、20~25g/LB、30~35g/LC、40~45g/LD、50~55g/LE、70~75g/L
- 血站办理再次执业登记,提交《血站再次执业登记申请书》及《血站执业许可证》。省级人民政府卫生行政部门应当根据血站业务开展和监督检查情况进行审核,审核合格的,予以继续执业。未通过审核的,应该如何办理()。A、没收其《血站执业许可证》B、注销其《血站执业许可证》C、责令停止执业D、再次进行审核,直到整改合格E、责令其限期整改;经整改仍审核不合格的,注销其《血站执业许可证》
- 单选题6阶有限群的任何子群一定不是( )阶。A 2B 3C 4D 6
- 一位献血者第一次来到某献血车去献血,但是他告诉医生他昨晚喝酒了,并且喝醉了,但是今天他坚持要献血。医生为他讲解献血前注意事项,不包括()。A、前一天不要饮食过饱B、睡眠充足C、献血前不要吃油腻的东西D、不要喝酒E、不要抽烟