网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
“数列”是高中数学必修5的内容。《普通高中数学课程标准(实验)》要求学生能“通过对日常生活中大量实际问题的分析,建立等差数列和等比数列这两种数列模型;在具体的问题情境中.发现数列的等差关系或等比关系,并能用有关知识解决相应的问题。”
(1)请设计一道能用等比数列知识解决的实际问题并求解;(20分)
(要求:给出问题情境;抽象出数量关系;建立数学模型;写出解答过程、讨论和反思。)
(2)根据上面的问题情境设计一道开放题或探索题。(10分)
(1)请设计一道能用等比数列知识解决的实际问题并求解;(20分)
(要求:给出问题情境;抽象出数量关系;建立数学模型;写出解答过程、讨论和反思。)
(2)根据上面的问题情境设计一道开放题或探索题。(10分)
参考答案
参考解析
解析:(1)①创设情境,提出问题
在古印度,有个名叫西萨的人,发明了国际象棋,当时的印度国王大为赞赏,对他说:我可以满足你的任何要求。西萨说:请给我棋盘的64个方格上,第一格放1粒小麦,第二格放2粒,第三格放4粒,往后每一格都是前一格的两倍,直至第64格。国王令宫廷数学家计算,结果出来后,国王大吃一惊。为什么呢
问题1:同学们,你们知道西萨要的是多少粒小麦吗
(设计意图:设计这个情境目的是在引入课题的同时激发学生的兴趣,调动学习的积极性。故事内容紧扣本节课的主题与重点。)
师生互动:引导学生写出麦粒总数l+2+22+23+……+263。带着这样的问题,学生会动手算了起来,他们想到用计算器依次算出各项的值,然后再求和。这时对他们的这种思路给予肯定。
(设计意图:在实际教学中,由于受课堂时间限制,教师舍不得花时间让学生去做所谓的无用功。急急忙忙地抛出“错位相减法”,这样做有悖学生的认知规律:求和就想到相加,这是合乎逻辑颀理成章的事,教师为什么不相加而马上相减呢 在这个教学关键处学生难以转过弯来,因而在教学中应舍得花时间营造知识形虞过程的氛围.突破学生学习的障碍。同时,形成繁难的情境激起了学生的求知欲,迫使学生急于寻求解决目囊的新方法,为后面的教学埋下伏笔。)
②师生互动,探究问题
在肯定他们的思路后,接着问:1+2+22+23+……+263是什么数列 有何特征 应归结为什么数学问题呢
学情预设:探讨1:设S64=1+2+22+23+……+263记(1)式,注意观察每一项的特征,有何联系 (学生会发现,后一项都是前一项的2倍)
探讨2:如果我们把每一项都乘以2,就变成了它的后一项,(1)式两边同乘以2则有2S64=2+22+23+.....263+264,记为(2)式。比较(1)(2)两式,你有什么发现
(设计意图:留出时间让学生充分地比较,等比数列前n项和的公式推导关键是变“加”为“减’.在教师看来这是“天经地义”的,但在学生看来却是“不可思议”的,因此教学中应着力在这儿做文章.从面抓住培养学生的辩证思维能力的良好契机。)
经过比较、研究,学生发现:(1)、(2)两式有许多相同的项,把两式相减,相同的项就消去了。得到:S64=264-1.老师指出:这就是错位相减法,并要求学生纵观全过程。
反思:为什么(1)式两边要同乘以2呢
(设计意图:经过繁难的计算之后,突然发现上述解法,不禁惊呼:真是太简单了!让学生在探索过程中,充分感受到成功的情感体验,从而增强学习数学的兴趣和学好数学的信心。)
③故事结束,首尾呼应
最后我们回到故事中的问题,我们可以计算出国王奖赏的小麦约为1.84×1019粒,大约7000亿吨,用这么多小麦能从地球到太阳铺设一条宽l0米、厚8米的大道,大约是全世界一年粮食产量的459倍,显然国王兑现不了他的承诺。
(设计意图:把引入课题时的悬念给予释疑,有助于学生克服疲倦、继续积极思维。)④教学反思对公式的教学,要使学生掌握与理解公式的来龙去脉,掌握公式的推导方法,理解公式的成立条件,充分体现公式之间的联系。在教学中,采用“问题——探究”的教学模式,把整个课堂分为呈现问题、探索规律、总结规律、应用规律四个阶段。
(2)引导学生将结论一般化,设等比数列{an},首项为a1,公比为q,如何求前项和Sn 这里,让学生自主完成.并喊一名学生上黑板,然后对个别学生进行指导。
(设计意图:在教师的指导下,让学生从特殊到一般,从已知到未知,步步深入,让学生自己探究公式,从而体验到学习的愉快和成就感。)
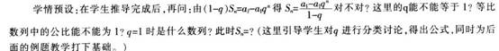
再次追问:结合等比数列的通项公式an=a1qn-1,如何把Sn用a1、an、q表示出来 (引导学生得出公式的另一形式)
(设计意图:通过反问精讲,一方面使学生加深对知识的认识,完善知识结构,另一方面使学生由简单地模仿和接受,变为对知识的主动认识,从而进一步提高分析、类比和综合的能力。这一环节非常重要,尽管时间有时比较少,甚至仅仅几句话,然而却有画龙点睛之妙用。)
在古印度,有个名叫西萨的人,发明了国际象棋,当时的印度国王大为赞赏,对他说:我可以满足你的任何要求。西萨说:请给我棋盘的64个方格上,第一格放1粒小麦,第二格放2粒,第三格放4粒,往后每一格都是前一格的两倍,直至第64格。国王令宫廷数学家计算,结果出来后,国王大吃一惊。为什么呢
问题1:同学们,你们知道西萨要的是多少粒小麦吗
(设计意图:设计这个情境目的是在引入课题的同时激发学生的兴趣,调动学习的积极性。故事内容紧扣本节课的主题与重点。)
师生互动:引导学生写出麦粒总数l+2+22+23+……+263。带着这样的问题,学生会动手算了起来,他们想到用计算器依次算出各项的值,然后再求和。这时对他们的这种思路给予肯定。
(设计意图:在实际教学中,由于受课堂时间限制,教师舍不得花时间让学生去做所谓的无用功。急急忙忙地抛出“错位相减法”,这样做有悖学生的认知规律:求和就想到相加,这是合乎逻辑颀理成章的事,教师为什么不相加而马上相减呢 在这个教学关键处学生难以转过弯来,因而在教学中应舍得花时间营造知识形虞过程的氛围.突破学生学习的障碍。同时,形成繁难的情境激起了学生的求知欲,迫使学生急于寻求解决目囊的新方法,为后面的教学埋下伏笔。)
②师生互动,探究问题
在肯定他们的思路后,接着问:1+2+22+23+……+263是什么数列 有何特征 应归结为什么数学问题呢
学情预设:探讨1:设S64=1+2+22+23+……+263记(1)式,注意观察每一项的特征,有何联系 (学生会发现,后一项都是前一项的2倍)
探讨2:如果我们把每一项都乘以2,就变成了它的后一项,(1)式两边同乘以2则有2S64=2+22+23+.....263+264,记为(2)式。比较(1)(2)两式,你有什么发现
(设计意图:留出时间让学生充分地比较,等比数列前n项和的公式推导关键是变“加”为“减’.在教师看来这是“天经地义”的,但在学生看来却是“不可思议”的,因此教学中应着力在这儿做文章.从面抓住培养学生的辩证思维能力的良好契机。)
经过比较、研究,学生发现:(1)、(2)两式有许多相同的项,把两式相减,相同的项就消去了。得到:S64=264-1.老师指出:这就是错位相减法,并要求学生纵观全过程。
反思:为什么(1)式两边要同乘以2呢
(设计意图:经过繁难的计算之后,突然发现上述解法,不禁惊呼:真是太简单了!让学生在探索过程中,充分感受到成功的情感体验,从而增强学习数学的兴趣和学好数学的信心。)
③故事结束,首尾呼应
最后我们回到故事中的问题,我们可以计算出国王奖赏的小麦约为1.84×1019粒,大约7000亿吨,用这么多小麦能从地球到太阳铺设一条宽l0米、厚8米的大道,大约是全世界一年粮食产量的459倍,显然国王兑现不了他的承诺。
(设计意图:把引入课题时的悬念给予释疑,有助于学生克服疲倦、继续积极思维。)④教学反思对公式的教学,要使学生掌握与理解公式的来龙去脉,掌握公式的推导方法,理解公式的成立条件,充分体现公式之间的联系。在教学中,采用“问题——探究”的教学模式,把整个课堂分为呈现问题、探索规律、总结规律、应用规律四个阶段。
(2)引导学生将结论一般化,设等比数列{an},首项为a1,公比为q,如何求前项和Sn 这里,让学生自主完成.并喊一名学生上黑板,然后对个别学生进行指导。
(设计意图:在教师的指导下,让学生从特殊到一般,从已知到未知,步步深入,让学生自己探究公式,从而体验到学习的愉快和成就感。)
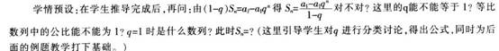
再次追问:结合等比数列的通项公式an=a1qn-1,如何把Sn用a1、an、q表示出来 (引导学生得出公式的另一形式)
(设计意图:通过反问精讲,一方面使学生加深对知识的认识,完善知识结构,另一方面使学生由简单地模仿和接受,变为对知识的主动认识,从而进一步提高分析、类比和综合的能力。这一环节非常重要,尽管时间有时比较少,甚至仅仅几句话,然而却有画龙点睛之妙用。)
更多 ““数列”是高中数学必修5的内容。《普通高中数学课程标准(实验)》要求学生能“通过对日常生活中大量实际问题的分析,建立等差数列和等比数列这两种数列模型;在具体的问题情境中.发现数列的等差关系或等比关系,并能用有关知识解决相应的问题。” (1)请设计一道能用等比数列知识解决的实际问题并求解;(20分) (要求:给出问题情境;抽象出数量关系;建立数学模型;写出解答过程、讨论和反思。) (2)根据上面的问题情境设计一道开放题或探索题。(10分)” 相关考题
考题
高中数学《等比数列》
一、考题回顾
二、考题解析
【教学过程】
(一)引入新课
利用多媒体放映具体实例:(1)细胞分裂模型。
提问:通过观察影片中的实例,你能用数字表达出上述实例的含义吗?
学生活动:学生通过观察计算,得出1,2,4,8,……
提问:这个数列是我们之前学过的等差数列吗?它又有什么特点呢?
引出《等比数列》。
(二)探索新知
1.等比数列的概念
大屏幕展示实例:(2)《庄子》中“一尺之棰”的论述。
1.既是等差数列又是等比数列的数列存在吗?如果存在,你能举出例子吗?
2.等比数列的性质有哪些?(至少说出3点)
考题
高中数学《等比数列前n项和》
一、考题回顾
题目来源:5月19日 上午 重庆市 面试考题
试讲题目
1.题目:等比数列前n项和
2.内容:
3.基本要求:
(1)引导学生应用等比数列前n项和;
(2)试讲10分钟;
(3)合理设计板书;
(4)要有适当的提问互动环节。
答辩题目
1.等差数列的前n项和公式是什么?
2.怎样才能设计好授课板书呢?你能给出几点建议吗?
考题
若在Excel2010中要分别进行等差数列2、4、6„和等比数列1、3、9„自动填充,则下列说法中不正确的是()。A、等差数列的公差是2,等比数列的公比是3B、数列的公差或公比不是填充“序列”对话框中的“步长值”C、操作时可单击“开始”选项卡→“编辑”组→“填充”→“系列”D、进行等差或等比数列填充时,既可选择行或列,也可选择填充序列对话框中的“终值”
考题
单选题若在Excel2010中要分别进行等差数列2、4、6„和等比数列1、3、9„自动填充,则下列说法中不正确的是()。A
等差数列的公差是2,等比数列的公比是3B
数列的公差或公比不是填充“序列”对话框中的“步长值”C
操作时可单击“开始”选项卡→“编辑”组→“填充”→“系列”D
进行等差或等比数列填充时,既可选择行或列,也可选择填充序列对话框中的“终值”
考题
问答题为什么在中学教学中,特别重视等差数列和等比数列?
热门标签
最新试卷