网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
由圈权值为9.2.5.7的四个叶子结点构造一颗哈夫曼树，该树的带权路径长度为()。

A.23
B.37
C.44
D.46

参考答案

参考解析
解析：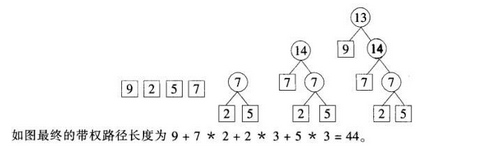
更多 “由圈权值为9.2.5.7的四个叶子结点构造一颗哈夫曼树，该树的带权路径长度为()。A.23 B.37 C.44 D.46” 相关考题
考题 由分别带权为9，2，5，7的四个叶子结点构成一棵哈夫曼树，该树的带权路径长度为( )。A．23B．37C．44D．46
查看答案
考题 由权值为9，2，5，7的四个叶子结点构造一棵哈夫曼树，该树的带权路径长度为(50)。A．23B．37C．44D．46
查看答案
考题 带权为9，2，4，6的4个叶子结点构造一棵哈夫曼树，该树的带权路径长度为______。A．21B．41C．36D．39
查看答案
考题 利用3、6、8、12这四个值作为叶子结点的权,生成一棵哈夫曼树,该树中所有叶子结点中的最长带权路径长度为()。 A.16B.30C.12D.18
查看答案
考题 利用3、 6、8、12这四个值作为叶子结点的权,生成一棵哈夫曼树,该树中所有叶子结点中的最长带权路径长度为( )。 A、18B、16C、30D、12
查看答案
考题 由值为29、12、15、6、23的五个叶子结点构造的哈夫曼树为(64)，其带权路径长度为(65)。A．B．C．D．
查看答案
考题 ● 由权值为 29、12、15、6、23 的五个叶子结点构造的哈夫曼树为（64)，其带权路径长度为 （65） 。
查看答案
考题 若以{4，5，6，3，8}作为叶子结点的权值构造哈夫曼树，则带权路径长度是(33)。A．55B．68C．59D．28
查看答案
考题 由分别带权9，2，3，5，6的五个叶子结点生成的哈夫曼树，该树的带权路径长度为A．50B．60C．55D．65
查看答案
考题 下列关于哈夫曼树的叙述错误的是A．一棵哈夫曼树是带权路径长度最短的二叉树B．一棵哈夫曼树中叶结点的个数比非叶结点的个数大1C．一棵哈夫曼树结点的度要么是0，要么是2D．哈夫曼树的根结点的权值等于各个叶子结点的权值之和
查看答案
考题 由权值为5，9，2，6的4个叶子构造一棵哈夫曼树，该树的带权路径长度为(59)。A．21B．22C．42D．44
查看答案
考题 由权值为9，2，5，7的四个叶子构造一棵哈夫曼树，该树的带权路径长度为(13)。A．23B．37C．44D．46
查看答案
考题 关于哈夫曼树，下列说法正确的是()。A.在哈夫曼树中，权值相同的叶子结点都在同一层上 B.在哈夫曼树中，权值较大的叶子结点一般离根结点较远 C.哈夫曼树是带权路径长度最短的树，路径上权值较大的结点离根较近 D.在哈夫曼编码中，当两个字符出现频率相同时，其编码也相同，对于这种情况应作特殊外理
查看答案
考题 下面关于哈夫曼树的说法，不正确的是（）A、对应于一组权值构造出的哈夫曼树一般不是唯一的B、哈夫曼树具有最小带权路径长度C、哈夫曼树中没有度为1的结点D、哈夫曼树中除了度为1的结点外，还有度为2的结点和叶结点
查看答案
考题 由带权为，9、2.5，7，的四个叶子结点构造一裸哈夫曼树.该树的带权路径长度为（）。
查看答案
考题 哈夫曼树是带权路径长度（）的树，通常权值较大的结点离根（）
查看答案
考题 由带权为3，9，6，2，5的5个叶子结点构成一棵哈夫曼树，则带权路径长度为（）。
查看答案
考题 若以4，5，6，7，8作为叶子结点的权值构造哈夫曼树，则其带权路径长度是（）。
查看答案
考题 哈夫曼树是带权路径长度最短的树，路径上权值较大的结点离根较近。
查看答案
考题 哈夫曼树是带权路径长度（）的树，通常权值较大的结点离根结点（）。
查看答案
考题 填空题由带权为，9、2.5，7，的四个叶子结点构造一裸哈夫曼树.该树的带权路径长度为（）。
查看答案
考题 单选题对哈夫曼树，下列说法错误的是（）。A 哈夫曼树是一类带树路径长度最短的树B 给出一组数，构造的哈夫曼树唯一C 给出一组数，构造的哈夫曼树的带树路径长度不变D 哈夫曼树的带权路径长度为每个叶子的路径长度与该叶子权值乘积之和
查看答案
考题 单选题利用3、6、8、12这四个值作为叶子结点的权，生成一棵哈夫曼树，该树中所有叶子结点中的最长带权路径长度为（）。A 16B 30C 12D 18
查看答案
考题 单选题下面关于哈夫曼树的说法，不正确的是（）A 对应于一组权值构造出的哈夫曼树一般不是唯一的B 哈夫曼树具有最小带权路径长度C 哈夫曼树中没有度为1的结点D 哈夫曼树中除了度为1的结点外，还有度为2的结点和叶结点
查看答案
考题 单选题利用3、8、12、6这4个值作叶子结点的权，生成一棵哈夫曼树，该树的带权路径长度为（）A 55B 29C 58D 38
查看答案
考题 填空题若以4，5，6，7，8作为叶子结点的权值构造哈夫曼树，则其带权路径长度是（）。
查看答案
考题 单选题由带权为9，2，5，7的四个叶子结点构造一棵哈夫曼树，该树的带权路径长度为（）。A 23B 37C 46D 44
查看答案
热门标签
最新试卷